Окружность

1. Построение отрезка равного данному

Изобразим фигуры, данные в условии: луч ОС и отрезок АВ.

Построение:

Построим окружность радиуса АВ с центром в точке О.

Окружность пересечет луч ОС в некоторой точке D.

Отрезок ОD – искомый.

2. Построение угла равного данному

Дано:

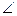А

Построить:

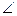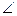А = О

Доказательство:

рассмотрим ΔАВС и ΔОDE.

1. АС=ОЕ, как радиусы одной окружности.

2. АВ=ОD, как радиусы одной окружности.

3. ВС=DE, как радиусы одной окружности.

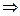
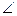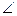ΔАВС = ΔОDЕ (по трем сторонам) А = О

Построение:

1. Построить произвольный луч.

2. Построить две равные окружности произвольного радиуса и окружность с центрами в начале луча и в вершине данного угла.

3. Найти и обозначить точки пересечения окружностей с лучом и со сторонами угла.

4. Построить окружность с центром в точке пересечения луча и окружности и радиусом, равным расстоянию между точками, построенными на сторонах угла.

5. Найти и обозначить точку пересечения окружностей.

6. Провести новый луч из начала луча через построенную точку пересечения окружностей.

7. Угол, образованный двумя построенными лучами, - искомый.

3. Построение биссектрисы угла

Дано:

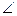А

Построить:

АВ - биссектриса

Доказательство:

Рассмотрим ∆АСВ и ∆ АDВ

1. АС=АD, как радиусы одной окружности.

2. СВ=DB, как радиусы одной окружности.

3. АВ – общая сторона.

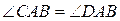∆АСВ = ∆ АDВ (по трем сторонам) луч АВ – биссектриса.

Построение:

1. Построить окружность произвольного радиусас центром в вершине угла.

2. Найти и обозначить точки пересечения окружности со сторонами угла.

3. Построить окружности с центрами в построенных точках и тем же радиусом.

4. Найти иобозначить точку пересечения окружностей.

5. Провести луч с началом в вершине угла через точку пересечения окружностей, - искомая биссектриса угла.

4. Построение перпендикулярных прямых

Случай

Дано:

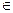М а

Построить:

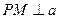
Доказательство:

1.АМ=МВ, как радиусы одной окружности.

2. АР=РВ, как радиусы одной окружности 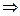∆АРВ р/б

3. РМ медиана в р/б треугольнике является также ВЫСОТОЙ.

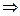
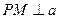
Случай

Дано:

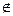М а

Построить:

Доказательство:

АМ=АN=MB=BN, как равные радиусы.

МN-общая сторона.

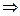∆MВN= ∆MAN (по трем сторонам)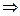

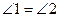
В р/б ∆АМВ отрезок МС является биссектрисой, а значит, и высотой.

Построение:

1. Построить окружность с центром в данной точке и радиусом больше расстояния от данной точки до прямой.

2. Найти и обозначить точки пересечения окружности с прямой.

3. Построить две равные окружности с центрами в построенных на прямой точках радиусом равным длине отрезка.

4. Найти и обозначить точку пересечения окружностей.

5. Провести прямую через данную точку, не лежащую на прямой и точку пересечения окружностей, - искомая прямая.

5.Построение середины отрезка

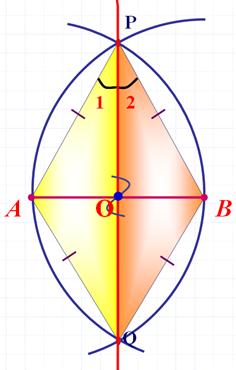Дано:

АВ

Построить:

О – середина отрезка АВ.

Доказательство:

∆АРQ = ∆ BPQ (по трем сторонам) .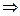

∆ АРВ р/б.

Отрезок РО является биссектрисой, а значит, и медианой.

Тогда, точка О – середина АВ.

Построение:

1. Построить две равные окружности с центрами в концах отрезка и радиусом равным АВ.

2. Обозначить точки пересечения окружностей.

3. Провести прямую через точки пересечения окружностей.

4. Обозначить точку пересечения прямой и отрезка, - искомая точка.

Date: 2015-04-23; view: 686; Нарушение авторских прав