Продолжение 25б

y²= 2px - (2) уравнение параболы

При переходе от (1) к (2) обе части уравнения один раз возводили в квадрат => могли появиться лишние корни. Надо доказать, что точка, коорд. которой удовлетворяют (2) принадлежит параболе.

Пусть M₀(x₀, y₀): y₀² = 2px₀

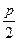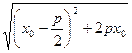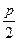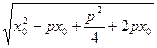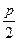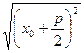|x₀+ |- =|x₀+ | - =|x₀+ |- =|x₀+ 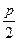|-|x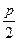₀+ |=0

Þ (2) – каноническое уравнение параболы

Опр.: Директрисой, соответствующей данному фокусу, гиперболы или параболы называют прямую перпендикулярную к фокальной оси, отстоящей от центра на расстояние a/e и лежащей с соответствующим ей фокусом по одну сторону от центра.

Уравнения директрисы x= 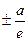. Для эллипса: e<1, 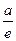>a. Для гиперболы: e>1, 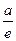<a

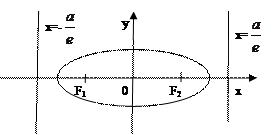
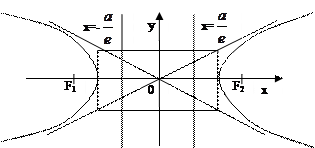
Для любой точки эллипса или гиперболы отношение расстояний до фокуса к расстоянию до соответствующей директрисы есть величина постоянная равная e

r=a-ex d= =>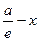

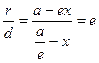
Опр.: Фокальным параметром кривой второго порядка называют половину длины фокальной хорды (проходящей через фокус перпендикулярно к оси)

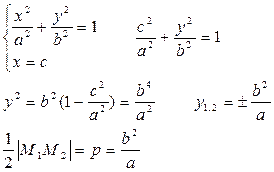
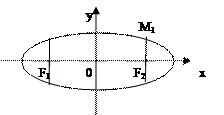
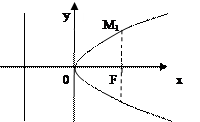
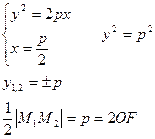
-фокальный параметр для эллипса и гиперболы. -фокальный параметр для параболы

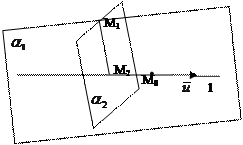Продолжение 26б