Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
II Векторное произведение
|
|
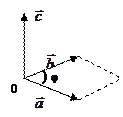Под векторным произведением двух векторов 
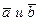понимается вектор 
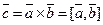, для которого:
1) модуль равен площади параллелограмма, построенного на данных векторах, т.е.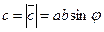 
, где j=a^b, (0£j£p)
2) этот вектор перпендикулярен перемножаемым векторам (иначе говоря, перпендикулярен плоскости построенного на них параллелограмма), т.е.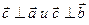 
.
3) если вектора не коллинеарные, то векторы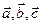 
, образуют правую тройку векторов.
Свойства:
1 При изменении порядка сомножителей векторное произведение меняет свой знак на противоположный, сохраняя модуль, т.е.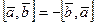 
(коммутативность не выполняется)
2 Векторный квадрат равен нуль-вектору, т.е.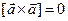 
3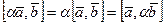 
линейность a=const
4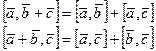 
дистрибутивность
5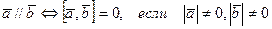 
Выражение векторного произведения через координаты векторов сомножителей
25 Вывод канонических уравнений эллипса, гиперболы, параболы.
Опр. Эллипсом называют геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух фиксированных точек плоскости (фокусов) есть величина постоянная, которую обозначают 2a.
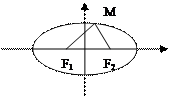
(M,F1)=r1, (M,F2)=r2 - фокальные радиусы точки М
М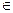 
эллипсу 
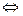r1+ r2=const=2a
(F1, F2) – фокальное расстояние |F1 F2|=2c
r1+ r2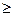 
|F1 F2| 2a 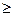2c (2a=2c 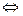M, F1, F2 – лежат на одной прямой)
a>c e=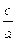 
<1 - эксцентриситет эллипса
Введем систему координат: за ось абсцисс примем прямую F1F2 (фокальная ось эллипса), за начало примем середину отрезка F1F2
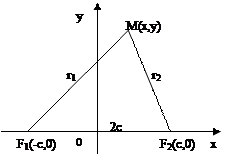Такая выбранная система координат называется канонической
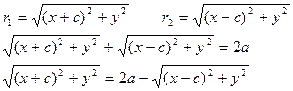
(1)- уравнение эллипса
Возведем в квадрат
(x+c)2 + y2 =4a2 +(x-c)2 + y2 -4a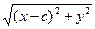 
4a2 -4xc -4a 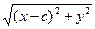=0
a2 -xc =a 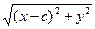Возведем в квадрат
a4 - 2a2xc + x2c2 = a2x2-2a2xc+ a2c2 +a2y2
a4 + x2c2 = a2x2+ a2c2 +a2y2
a2(a2- c2) = x2 (a2 -c2) +a2y2 (т.к. a>c => a2 -c2 >0 обозначим a2 -c2 = b2)
a2b2= x2 b2 +a2y2 или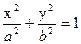 
- (2) уравнение эллипса
При переходе от (1) к (2) обе части уравнения два раза возводили в квадрат => могли появиться лишние корни. Надо доказать, что точка, коорд. которой удовлетворяют (2) принадлежит эллипсу.
Пусть M0(x0, y0):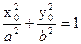 
=> y02=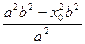 
Надо доказать (M0,F1)+ (M0,F2) =2a
(M0,F1)=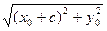 
; (M0,F2) =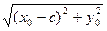 
(M0 ,F1)=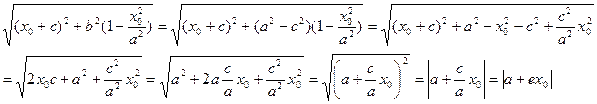 
(M0,F2) = | a – ex 0 |
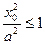
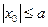и e<1 => | ex 0|<a => a – ex 0>0 и a + ex 0 >0
(M0,F1)= a + ex 0 (M0,F2)= a – ex 0
a + ex 0+ a – ex 0 =2a
ð (2) – каноническое уравнение эллипса
Фокальные радиусы: r1 = a + ex ; r2 = a – ex
Опр. Гиперболой называют геометрическое место точек плоскости, для каждой из которых модуль разности расстояний до двух фиксированных точек плоскости (фокусов) есть величина постоянная, которую обозначают 2a.
(M,F1)=r1, (M,F2)=r2 - фокальные радиусы точки М
М 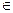гиперболе |r1- r2 |=const=2a
(F1, F2) - фокальное расстояние |F1 F2|=2c
|r1- r2|<2c a<c e = 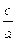> 1 - эксцентриситет гиперболы
Введем систему координат: за ось абсцисс примем прямую F1F2 (фокальная ось эллипса), за начало примем середину отрезка F1F2
Date: 2015-04-23; view: 586; Нарушение авторских прав