Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Классификация кривых второго порядка
|
|
Первая кв. форма поверхности, ее применения.
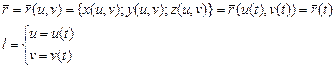– радиус вектор
- уравнение линии лежащей на поверхности
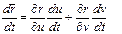- касательный вектор к линии, лежащий на поверхности
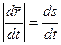, где s – длина дуги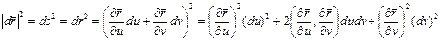 
Вводя обозначения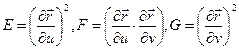 
получим первую квадратичную форму поверхности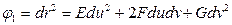 
Отметим некоторые свойства:
1. 
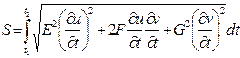- линейный элемент поверхности. Говорят, что 
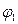определяет метрику поверхности
2. Тождество Лагранжа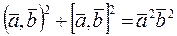 
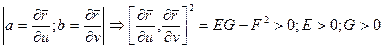т.е. 
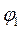положительна определена
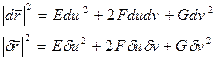
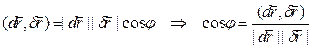
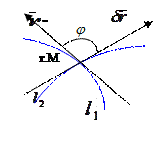
Найдем выражение cos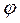 
через коэффициенты I кв. формы
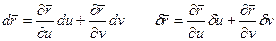
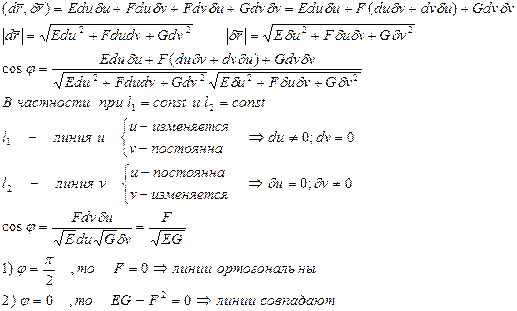
Классификация кривых второго порядка
– уравнение кривой второго рода
Используя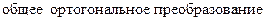 
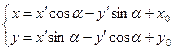
приходим к виду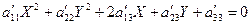 
Опр.: Целая рациональная функция от коэффициентов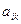 
называется инвариантом относительно некоторой преобразованной системы координат, если ее значение не меняется при переходе от данной системы к преобразованной, т.е. 
.
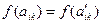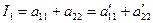
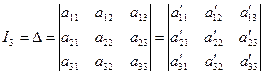
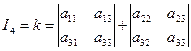
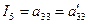
K – инвариант только для линии 3-го типа
Составляем характеристическое уравнение
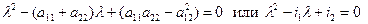
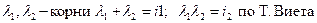
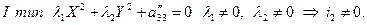
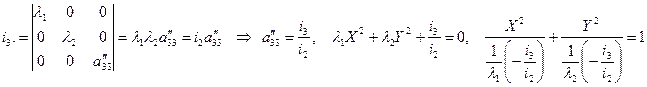
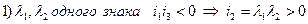
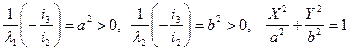
Вывод: для того, чтобы линия 1-го типа была действительным эллипсом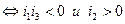 
.
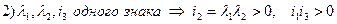
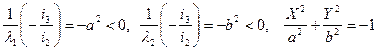
Вывод: для того, чтобы линия 1-го типа была мнимым эллипсом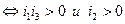 
.
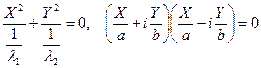
Вывод: для того, чтобы линия 1-го типа была точкой в области действительных чисел или парой мнимых пересекающихся прямых 
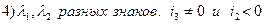
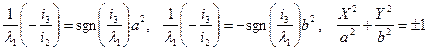
Вывод: того, чтобы линия 1-го типа была гиперболой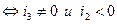 
Date: 2015-04-23; view: 761; Нарушение авторских прав