
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

III Векторно-скалярное или смешанное произведение
|
|
Опр3: Под смешанным (или векторно-скалярным) произведением векторов 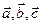 понимается число
понимается число 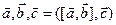
Построим параллелепипед П, ребрами которого, исходящими из общей вершины О, являются векторы 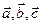

Тогда 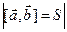 представляет собой площадь параллелепипеда, построенного на векторах
представляет собой площадь параллелепипеда, построенного на векторах 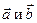 , т.е. площадь основания параллелепипеда. Высота этого параллелепипеда Н равна
, т.е. площадь основания параллелепипеда. Высота этого параллелепипеда Н равна 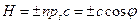 , где
, где 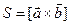 и знак плюс соответствует острому углу j=Ð(c, S), а знак минус – тупому углу j. В первом случае векторы
и знак плюс соответствует острому углу j=Ð(c, S), а знак минус – тупому углу j. В первом случае векторы 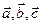 образуют правую тройку, во втором – левую тройку.
образуют правую тройку, во втором – левую тройку.
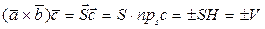 , где объем параллелепипеда, построенного на векторах
, где объем параллелепипеда, построенного на векторах 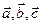 , т.е. смешанное произведение трех векторов равно объему V параллелепипеда, построенного на этих векторах, взятому со знаком плюс, если эти векторы образуют правую тройку, и со знаком минус, если они образуют левую тройку.
, т.е. смешанное произведение трех векторов равно объему V параллелепипеда, построенного на этих векторах, взятому со знаком плюс, если эти векторы образуют правую тройку, и со знаком минус, если они образуют левую тройку.
Свойства смешанного произведения:
1 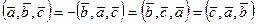 некоммутативность
некоммутативность
2 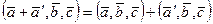 дистрибутивность
дистрибутивность
3 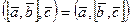 транзитивность
транзитивность
4 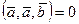
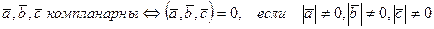 5
5
Выражение смешанного произведения через координаты векторов сомножителей
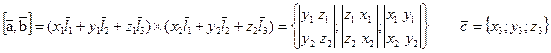
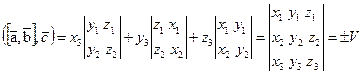
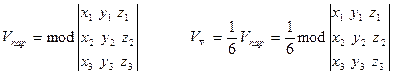
Продолжение 25а
Такая выбранная система координат называется канонической
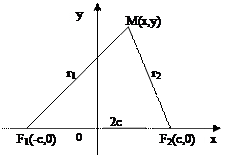 F1(-c,0), F2(c,0), M(x,y)
F1(-c,0), F2(c,0), M(x,y)
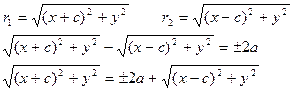
(1)- уравнение гиперболы
Возведем в квадрат
(x+c)2 + y2 =4a2 +(x-c)2 + y2 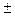 4a
4a 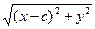
4a2 -4xc 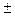 4a
4a 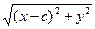 =0
=0
xc-a2 = 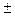 a
a 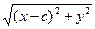 Возведем в квадрат
Возведем в квадрат
a4 - 2a2xc + x2c2 = a2x2-2a2xc+ a2c2 -a2y2
a4 + x2c2 = a2x2+ a2c2 -a2y2
a2(с2- a2) = x2 (c2 -a2) -a2y2 (т.к. c>a => c2 -a2 >0 обозначим c2 -a2 = b2)
a2b2= x2 b2 -a2y2 или 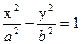 - (2) уравнение гиперболы
- (2) уравнение гиперболы
При переходе от (1) к (2) обе части уравнения два раза возводили в квадрат => могли появиться лишние корни. Надо доказать, что точка, координаты которой удовлетворяют (2) принадлежит гиперболе.
Пусть M0(x0, y0): 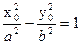 => y02=
=> y02= 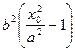
Надо доказать |  (M0,F1) -
(M0,F1) -  (M0,F2)| =2a
(M0,F2)| =2a
 (M0,F1)=
(M0,F1)= 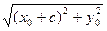 ;
;  (M0,F2) =
(M0,F2) = 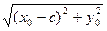
 (M0 ,F1)=
(M0 ,F1)= 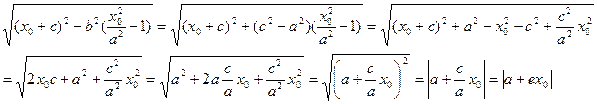
 (M0,F2) = | a – ex 0 |
(M0,F2) = | a – ex 0 |
| x 0>0 | x 0 <0 |
| r1 = a + ex0 | r1 = -a - ex0 |
| r2 = ex0 -a | r2 = a - ex0 |
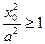
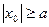 и e>1 => | ex 0|>a =>
и e>1 => | ex 0|>a =>
|r1 – r2 | =2a
Þ (2) – каноническое уравнение гиперболы
| x >0 правая ветвь | x <0 левая ветвь |
| r1 = a + ex | r1 = -(a- ex) |
| r2 = -(a - ex) | r2 = a – ex |
Фокальные радиусы:
Опр3. Параболой называют геометрическое место точек плоскости равноудаленных от фиксированной точки плоскости (фокуса) и от фиксированной прямой плоскости (директрисы).
 (M,F)=r - фокальный радиус точки М,
(M,F)=r - фокальный радиус точки М,  (M,l)=d – расстояние до директрисы
(M,l)=d – расстояние до директрисы
М 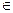 параболе
параболе 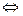 r=d
r=d
 (F, l) =p- фокальный параметр параболы
(F, l) =p- фокальный параметр параболы
e =  = 1 – эксцентриситет параболы
= 1 – эксцентриситет параболы
d=|x + 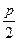 | r=
| r= 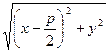
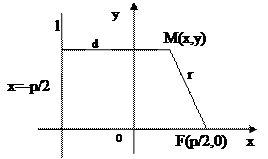
|x + 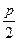 | =
| = 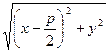 (1)- уравнение параболы
(1)- уравнение параболы
Возведем в квадрат
x2 +xp+ 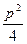 =x2 –xp+
=x2 –xp+ 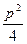 + y2 (продолжение на след листке)
+ y2 (продолжение на след листке) 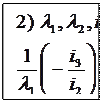
Date: 2015-04-23; view: 708; Нарушение авторских прав