
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Изображение пространственных фигур на плоскости
|
|
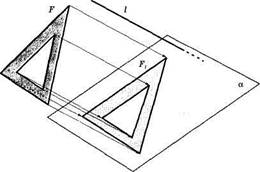
Для изображения пространственных фигур на плоскости обычно пользуются параллельным проектированием. Объясним этот способ изображения фигуры. Пусть даны плоскость а и пространственная фигура F (рис. 21). Берем произвольную прямую U пересекающую плоскость а. Проведем через каждую точку фигуры F прямую, параллельную I. Точки пересечения всех этих прямых с плоскостью а образуют плоскую фигуру Fr
|
Полученную таким образом фигуру Fx называют параллельной проекцией (изображением) фигуры F на плоскость при проектировании параллельно /. При этом прямую I называют проектирующей прямой
плоскость а— плоскостью проекций (плоскостью чертежа).
Такой способ изображения пространственной фигуры на плоскости соответствует зрительному восприятию фигуры при рассматривании ее издали. Отметим некоторые свойства изображения фигуры на плоскости, вытекающие из описанного
|
ее построения.
Теорема 12 (о проекциях отрезков). Если проектируемые отрезки не параллельны проектирующей прямой, то:
1) проекцией отрезка является отрезок;
2) параллельные отрезки проектируются в параллельные отрезки
или отрезки одной прямой;
3) длины проекций параллельных отрезков или отрезков одной
прямой относятся как длины проектируемых отрезков.
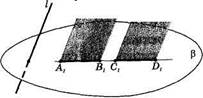
Доказательство. 1) Все прямые, параллельные проектирующей прямой I и пересекающие данный отрезок АВ, заполняют полосу а —часть плоскости, ограниченную параллельными прямыми ААХ и ВВХ. Полоса а пересекает плоскость проекций (} по отрез jj. Этот отрезок — проекция отрезка АВ на плоскость (3 (рис.22).
Пусть проектируемые отрезки АВ и CD параллельны. Все
пересекающие их прямые, параллельные I, заполняют полосы а и
у — части одной плоскости (рис. 23) или параллельных плоскостей.
Полосы а и у пересекают плоскость (5 соответственно по отрезкам
2) одной прямой или по параллельным отрезкам А1В1 и C1D1 — проек
циям данных отрезков на плоскость |3.
3) а) Если проектируемые отрезки АВ и CD расположены на
одной прямой (рис.22), то [AjBJ: ICjDJ = |АВ|: \CD\( по теореме Фалеса).
б) Если отрезки АВ и CD параллельны, а их проекции А^В^ и
— параллелограмм.
ClDl лежат на одной прямой (рис. 23), то
 В этом случае: 1АД1: ICjDJ = [А.Д1: \CD\ = = |АВ|: |CD|.
В этом случае: 1АД1: ICjDJ = [А.Д1: \CD\ = = |АВ|: |CD|.
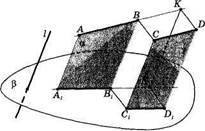
в) Если проекции AJZX и C^DX данных параллельных отрезков АВ и CD не лежат на одной прямой (рис. 24), то построим параллелограмм CDKB. Его проекция— параллелограмм Cfi^B^ Значит,
= |АВ|: \ВК\ = \АВ\: \CD\.
\AB\: \CD\, т.е. длины проекций парал- или отрезков одной прямой относятся как длиныотрепков.
Проекцией середины отрезка является середина шпроекции.
I 'посмотренные свойства параллельного проектирования отрезков ИО11ИОЛНЮТ наглядно и с большей определенностью изображать монлоские фигуры на плоскости.
Изображением фигуры называют любую плоскую фигуру, подобную проекции данной фигуры на некоторую плоскость.
Из теоремы о проекциях отрезков следует, что треугольник, в том числе равносторонний, равнобедренный и прямоугольный, можно изображать произвольным треугольником. Параллелограмм, в том числе ромб, прямоугольник, квадрат, можно изображать произвольным параллелограммом.
Date: 2015-04-23; view: 2216; Нарушение авторских прав