
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Параллельные и скрещивающиеся прямые
|
|
В пространстве две прямые могут лежать в одной плоскости, а могут и не лежать (в одной плоскости). Например, рассмотрим куб ABCD A1B1CiD1
Его ребра — отрезки, которые могут быть
продолжены в виде прямых отрезков. Видно, \с £>
что среди этих прямых имеются также не
пересекающиеся и не лежащие в одной
плоскости пары прямых. Например, АВ и А^
или ВС и AjBj.
Определение. Двепрямые, которыенележатводнойплоскости, называются скрещивающимися (рис. 10,а)
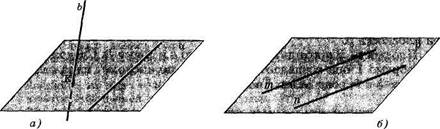
В рассматриваемом примере пары АВ, AiD1 и ВС, А1В1 являются примерами скрещивающихся прямых.
Две прямые в плоскости параллельны или пересекаются — третьей возможности для них нет. Например, в рассмотренном кубе стороны АВ и ВС, лежащие в одной плоскости, пересекаются в точке В, а стороны АВ и DC не пересекаются.
Опр е де ление. Две прямые называются параллельными, если они лежат в одной плоскости и не пересекаются (рис. 10, б).
В приведенном выше примере АВ и DC параллельны. Параллельность прямых обозначается в пространстве так же, как на плоскости ((AB)||(DC)). Отрезки (лучи), принадлежащие параллельным прямым, называются параллельными.
Из определения следует, что через две параллельные прямые всегда можно провести плоскость, причем только одну. Ведь если допустить, что через параллельные прямые а и Ъ проведены две различные плоскости, из этого следовало бы, что через прямую и некоторую точку прямой проведены две различные плоскости. Но этого не может быть (теорема 1). Итак, к перечисленным способам задания плоскости
Плоскость можно однозначно задать двумя через данную точку можно провести не параллельной данной (аксиома параллельных КО таких прямых можно провести в пространстве Через точку вне данной прямой можно провести Щ(ШЩ/т, параллельную этой прямой, и притом только одну.

|
| Рис.11 |
Доказательство. Обозначим данную прямую через а, данную точку через В. Через прямую и точку В можно провести единственную плоскость (теорема 1). Обозначим ее через а (рис. 11). Проведем через точку В в плоскости а прямую Ь, параллельную а. Докажем, что прямая Ъ, параллельная о, единственна.
Допустим, что существует другая прямая bv проходящая через точку В и параллельная прямой а. Через прямые а и & можно провести плоскость р.
Плоскость В проходит через прямую а и точку В. Следовательно, по теореме 1 она совпадает с а. Теперь по аксиоме параллельные прямые Ъ и Ъх совпадают. Теорема доказана.
Date: 2015-04-23; view: 1139; Нарушение авторских прав