
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Перпендикуляр и наклонная
|
|
О пределение. Перпендикуляром, опущенным из даннойточки на данную плоскость, называется отрезок, соединяющий данную точку с точкой плоскости, лежащей на прямой, перпендикулярной к плоскости.
Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра.
На рисунке 40 даны: точка С и плоскость ос. Прямая I проведена перпендикулярно к плоскости а. Отрезок CD — перпендикуляр, опущенный из точки С к плоскости а. Точка D — основание перпендикуляра.
Определение. Наклонной называют отрезок, один конец которого лежит в плоскости и не является перпендикуляром к данной плоскости (рис. 41).
Конец отрезка, лежащий в плоскости, называется основанием наклонной. А отрезок, соединяющий основание перпендикуляра и наклонной, проведенных из данной точки, называется проекцией наклонной.
На рисунке 41 изображены перпендикуляр CD, проведенный из точки С к плоскости а, наклонная CN и ее проекция DN.
| \с |
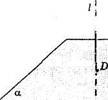 Длина отрезка CD на рисунках 40, 41 — расстояние от точки С до плоскости а.
Длина отрезка CD на рисунках 40, 41 — расстояние от точки С до плоскости а.
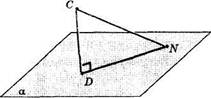
| Рис. 41 |
Рис. 40
Перпендикуляр CD меньше, чем наклонная CN, т.е. | CD | < | CN |. Действительно, в прямоугольном треугольнике CDN CD — катет, CN— гипотенуза. Итак, перпендикуляр, проведенный из данной точки к плоскости, меньше любой наклонной, проведенной из этой же точки к данной плоскости. Поэтому для расстояния от точки до плоскости дается следующее определение.
Определение. Расстояние.» от точки до плоскости называется длина перпендикуляра, опущенного из этой точки на плоскость.
Выше, когда говорилось о проекции наклонной, речь шла о прямоугольной проекции наклонной. Такие проекции получают при условии, что все проектирующие прямые перпендикулярны к плоскости проекций. Прямоугольное проектирование (или ортогональное проектирование) — один из видов параллельного проектирования.
В дальнейшем, говоря о проекциях, мы в основном будем иметь в виду только прямоугольные проекции.
Date: 2015-04-23; view: 1523; Нарушение авторских прав