Перпендикулярность прямой и плоскости

Определение. Прямая называется перпендикулярной к плос­кости, если онаперпендикулярна клюбойпрямой, лежащей в плоскости, проходящей через точку пересечения.

В этом случае и плоскость будет перпендикулярна к пря­мой: а± а и а± а (рис. 33).

Отрезок (луч) называется перпендикулярным к плоскос-

а ^k\ / ти, если он лежит на прямой,

перпендикулярной к данной плоскости.

Теорема 14 (признак перпендикулярности прямой и плоскости). Если прямая, пере­секающая плоскость, перпендикулярна к двум прямым этой плоскости, проходящим через точку пересечения, то она перпен­дикулярна к плоскости.

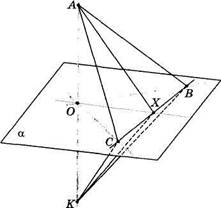
Рис.34

Доказательство. Пусть прямая АО, пересекающая плос­кость а в точке О, перпендику­лярна к прямым ОВ и ОС этой плоскости (рис. 34). Докажем, что прямая АО перпендикулярна к любой прямой ОХ, лежащей в плоскости а. Для этого проведем произвольную прямую, пересе­кающую прямые ОВ, ОС и ОХ в точках В, С и X А на прямой О А в разные стороны от О отложим равные отрезки ОА и ОК. Сое­динив отрезками точки Am К с точками В, С, X, получим не­сколько пар треугольников. Тре­угольники АВК и АСК равно­бедренные, так как их медианы 34

 

 

ВО и СО являются и высотами. Значит, |АВ| = \ВЩ, \АС\ = \СК\ и треугольники ABC и ВСК равны по трем сторонам, поэтому ZABC = = ZKBC. Равны и треугольники АВХ и КВХ по двум сторонам и углу между ними. Следовательно, \АХ\ = \КХ\. Так как треугольник АХК —-равнобедренный, то его медиана ХО является и высотой, т.е. (АО) 1 (ХО). А это значит, согласно определению, прямая ОА перпен­дикулярна к плоскости а. Теорема доказана.

Задача 1. Через данную точку прямой провести перпенди­кулярную ей плоскость.

Решение. Пусть а — данная прямая и А— точка на ней (рис. 35). Проведем через прямую а две плос­кости. Проведем в этих плоскостях через точку А прямые Ъ и с, перпен­дикулярные к прямой а. Плоскость, проходящая через эти прямые, перпендикулярна к прямой а по теореме 14.

Вопросы и задания

1. Что называется углом между скрещивающимися прямыми?

2. Какие прямые в пространстве называются перпендикулярными?

3. Верно ли утверждение, что "перпендикулярные прямые лежат в одной плос­
кости"?

4. В каких условиях прямая перпендикулярна к плоскости?

5. Прямая а перпендикулярна к плоскости а. Могут ли существовать в плоскости
прямые, не перпендикулярные к прямой а?

6. Докажите теорему о признаке перпендикулярности прямой и плоскости.

7. В каких условиях отрезок (луч) перпендикулярен к плоскости?

8. В окружающей обстановке найдите примеры взаимно перпендикулярных пря­
мых и прямой, перпендикулярной к плоскости.

Задачи

87. ABCDAJip^D^ — куб. Найдите угол между прямыми ВВ₁ и AD_V

88. ABCDAJS_lC_lD₁ — куб. Найдите угол между скрещивающимися
прямыми ADj и В_ХС.

89. Сколько прямых, перпендикулярных к данной прямой, можно
провести через данную на этой прямой точку? А через точку, не
лежащую на данной прямой?

90. Даны плоскость а и параллельная ей прямая а. Сколько прямых,
перпендикулярных к прямой о, можно провести в плоскости а?

92. ABCD — квадрат в плоскости о, его диагонали пересекаются в
точке О. Прямая а проходит через точку О и перпендикулярна к
плоскости а. Точка Е лежит на прямой о. Длина диагонали
квадрата равна 6 см, а \ОЕ\ = 4 см. Найдите расстояние от точки Е
до вершин квадрата.

93. ABCD — ромб в плоскости а. О — точка пересечения диагоналей
ромба. Прямая d перпендикулярна к плоскости а и проходит через
точку О.Е — точка прямой d. Найдите расстояние от точки Ело
вершин ромба, если | ОЕ | = 8 см, | АВ | = 12 см и один из углов
ромба равен 60°.

В

94. Даны четыре прямые: d\\d_l и l\\ l_v Докажите, что если d± l, то
d,Ll_v

95. Если ZAOB = ZAOC=50°, то могут ли быть перпендикулярными
прямые OS и ОС?

96. Лучи ОА, ОВ и ОС попарно перпендикулярны. Найдите периметр
треугольника ABC, если: а) \ОА\ = \ОВ\ = |ОС| = 5 см; б) \ОА\ = \ОВ\ =
= \ОС\ = а; в) \ОА\ = \ОВ\ = 3 дм, \ОС\ = 4 дм.

97. Существует ли замкнутая неплоская ломаная из пяти звеньев,
каждое звено которой перпендикулярно смежному?

98. В правильном тетраэдре ABCD середины сторон АВ и CD обо­
значены через Е и F. Докажите, что (EF) 1 (АВ) и (EF) 1 (CD). Если
\АВ\ = 4 см, то найдите длину отрезка EF.

99. Если ZMON = 30°, Z.MOE = 40°, то могут ли быть перпендику­
лярными прямые ON и ОШ

Date: 2015-04-23; view: 1808; Нарушение авторских прав