
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Признак параллельности прямых
|
|
Теорема 5. Две прямые, параллельные третьей прямой, параллельны.
Доказательство. Пусть Ъ\\ а, с\\ а Докажем, что прямые бис параллельны. Соответственно определению надо доказать, что: 1) Ъ и с лежат в одной плоскости; 2) прямые & и с не пересекаются.
| а) |
Предположим, что наши прямые не лежат в одной плоскости. Пусть а — плоскость, в которой лежат прямые а и Ъ, а В — плоскость, в которой лежат прямые а и с. Плоскости ос и В различны Отметим на прямой Ъ какую-нибудь точку В и проведем плоскость Р; через прямую с и точку В. Она пересечет плоскость а по прямой Ъх
Прямая Ьг не пересекает плоскость В. Если предположим, что пересекает, то точка пересечения должна принадлежать прямой а, так как прямые Ъг и а лежат в плоскости а. С другой стороны, она должна лежать и на прямой с, так как она будет общей точкой плоскостей р,, р (потому что по построению с — общая прямая плоскостей Pt, P). Но это невозможно, так как прямые а и с параллельны. Значит, прямая Ъх не пересекает плоскость р.
Так как прямая Ъх лежит в плоскости а и не пересекает прямую
а, то она параллельна а, а значит, совпадает с Ъ по аксиоме парал
лельных прямых. Таким образом, прямая Ъ, совпадая с прямой Ьх,
лежит в одной плоскости с прямой с (в плоскости Pj) и не пересекает
ее. Значит, прямые & и с параллельны. Теорема доказана.
Вопросы и задания
1. Какие прямые называются скрещивающимися?
2. Какие прямые в пространстве называются параллельными?
3. Что можно сказать об отрезках, принадлежащих параллельным прямым?
4. Дан куб ABCDAj.BjCj.Dj:
а) Укажите и обозначьте параллельные ребра куба. Сколько в кубе ребер,
параллельных одному ребру?
б) Укажите ребра, которые лежат на скрещивающихся прямых. Сколько ребер
скрещиваются с одним ребром? Обозначьте.
5. Докажите, что через точку вне данной прямой можно провести прямую, парал
лельную этой прямой, и притом только одну.
б. Объясните теорему о трех параллельных прямых в пространстве.
Задачи
|
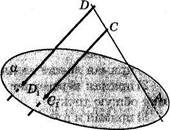
| Рис- 13 |
21.Прямые а и & параллельны, a b и с не параллельны. Докажите,
что прямые а и с не параллельны.
22.Отрезки ОА и ОВ пересекают плоскость а в точках Ах и Вг,
являющихся серединами этих отрезков. Найдите расстояние АВ,
если lAjBjhe.e см.
23.Прямые DDj и ССХ, изображенные на
рисунке 13, пересекают прямую AXD
в точках D и С, а плоскость а — в
точках Dj и Сг. Параллельны ли
прямые DD^ и СС^ Если да, то почему?
24.Прямые АВ и CD параллельны. Могут
ли быть скрещивающимися прямые
АС и BD? А пересекающимися?
25.Прямые MN и EF скрещиваются. Мо
гут ли быть параллельными прямые
ME и NF? А пересекающимися?
26.Прямые Ь и d скрещиваются. Что можно сказать о прямых а и с,
если a\\bnc\\d?
27.Прямые b и искрещиваются. Как будут расположены прямые b
и с, если для с выполняется условие: с\\ а"1
28.Даны две не совпадающие параллельные прямые. Докажите, что
все прямые, пересекающие данные две прямые, лежат в одной
плоскости.
29.Прямые АВ и CD пересекаются. Докажите, что прямые АС и CD
не скрещиваются.
30.Вершины треугольника ABC — середины отрезков OAV OBV OCV
Точка О принадлежит плоскости треугольника ABC. Во сколько
раз периметр треугольника А1В1С1 больше периметра
треугольника ABC?
31. ABCDA1B1C1D1 — куб. Докажите, что плоскость треугольника
АСС1 проходит через точку Av
32.Из точек Am В плоскости а проведены вне нее параллельные
отрезки: \АЩ = 16 см и \ВМ\ =12 см. Прямая МК пересекает
плоскость а в точке С. Найдите расстояние АС, если [АВ\ =9 см.
Рассмотрите оба случая.
33.Точка С делит отрезок АВ в отношении \АС\: \ВС\ = 2:3. Парал
лельные прямые, проходящие через точки А, В, С, пересекают
некоторую плоскость в точках А,В,С. Найдите отношение
34.Докажите, что середины сторон пространственного четырех
угольника являются вершинами параллелограмма (вершины
пространственного четырехугольника не лежат в одной
плоскости).
35.Докажите, что если прямые АВ и CD — скрещивающиеся, то
прямые АС л BD тоже скрещиваются.
Date: 2015-04-23; view: 1275; Нарушение авторских прав