
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Свойства перпендикулярных прямой и плоскости
|
|
Теорема 15. Если плоскость перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой.
Доказательство. Пусть а || о2 и а 1 ос. Докажем, что аг L а (рис. 36). Так как а 1 а, то в плоскости а найдутся пересекающиеся в точке А прямые бис, перпендикулярные а (по определению). Так как Ьис перпендикулярны к прямой а, то по теореме 13 они перпендикулярны и к прямой av параллельной а. Поэтому по теореме 14 а: ± а. Теорема доказана.
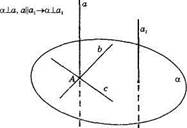
| Рис. 36 |
Рис. 37
Теорема 16 (обратная теорема). Две прямые, перпендикулярные к одной плоскости, параллельны.
Доказательство. Пусть Докажем, что а \\ Ь (рис. 37). Допустим, что прямые а и Ъ не параллельны. Выберем на прямой Ъ точку D, не лежащую в плоскости а. Проведем через точку D прямую bv параллельную прямой а. Так как a L а, то и fcx ± а (по теореме 15). Если Вт С — точки пересечения прямых Ъ и Ъг с плоскостью а, то из предположения следует, что в треугольнике BDC два прямых угла. Этого не может быть. Значит, прямые а и 6 параллельны. Теорема доказана.
|
Задача 2. Через точку А данной плоскости а провести перпендикулярную ей прямую.
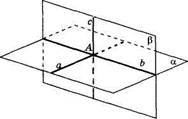
| Рис. 38 |
Решение. В плоскости а через точку А проведем прямую а (рис. 38). Через точку А проведем плоскость Д перпендикулярную к прямой а (задача 1). Пусть a n р = Ъ. В плоскости р через точку А проведем прямую с, перпендикулярную прямой Ь. Отсюда с L Ъ и с J. а. По признаку перпендикулярности прямой и плоскости (теорема 14) cL a. Итак, с — искомая прямая. Методом от противного можно доказать и единственность этой прямой.
Вопросы и задания
1. Докажите (теорему), что если плоскость перпен
дикулярна одной из двух параллельных прямых, то
она перпендикулярна и к другой.
2. Докажите (теорему), что две прямые, перпендику
лярные одной и той же плоскости, параллельны.
3. На рисунке 39 изображен прямоугольный парал
лелепипед. Используя рисунок, ответьте на вопросы:
1) К каким ребрам перпендикулярно основание ABCD?
2)Назовите пару ребер, перпендикулярных к грани ADDjA^.
4. В окружающей обстановке найдите примеры на свойства перпендикулярности прямой и плоскости.
Задачи
100. Сколько прямых, перпендикулярных к данной плоскости, можно
провести через данную точку? А отрезков?
101. а 1а. Как расположены относительно плоскости ос прямые, пер
пендикулярные к прямой а?
102.Постройте сечение куба плоскостью, проходящей через середину
его ребра перпендикулярно к этому ребру. Найдите площадь
сечения, если ребро куба равно 3 см.
103.Плоскость а перпендикулярна к катету МК прямоугольного тре
угольника MNK и делит его в отношении |MMJ: \MtK\ = 3:2.
В каком отношении плоскость а делит гипотенузу MN?
В
104.Расстояния от точки Р до всех вершин квадрата равны, точка О —
центр квадрата. Докажите, что прямая РО перпендикулярна к
плоскости квадрата.
105.Постройте сечение правильного тетраэдра плоскостью, перпен
дикулярной к ребру и проходящей через середину этого ребра.
Найдите площадь сечения, если ребро тетраэдра равно 8 см.
106.Прямые АА1 и BBV перпендикулярные к плоскости а, пересекают
ее в точках Ах и Blt а прямая АВ — в точке С. Найдите расстояние
AjBj, если [AAJ = 12 см, \BBt\ = 4 см, \В£\ = 2 см.
107.Треугольник ABC — равносторонний, а отрезок АО перпенди
кулярен к его плоскости. Найдите периметр и площадь треуголь
ника ОВС, если: 1) \АВ\ = 6 см, \АО\ = 8 см; 2) \АВ\ = \АО\ = о.
108. Прямые АА1 и BBV перпендикулярные к плоскости а, пересекают ее в точках А1 и Bv а прямая АВ — в точке С. Найдите расстояние Bfi, если \ААХ\ = 12 см, IAjSJ = \ВВг\ = 3 см.
Date: 2015-04-23; view: 2123; Нарушение авторских прав