
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Полупространства
|
|
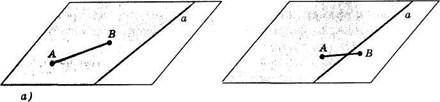
Вспомним, что каждая прямая в плоскости делит ее на две полуплоскости, для которых она служит общей границей. Полуплоскость, ограниченная прямой о, характеризуется следующими свойствами:
1. Она содержит прямую о;
Если обе точки Аи В принадлежат полуплоскости, но не прямой
1. а, то отрезок АВ не имеет общих точек с прямой а (рис. 6,о);
|
| б) |
| Рис. 6 |
3. Если же точка А принадлежит полуплоскости, а В ей не
принадлежит, то отрезок АВ имеет с прямой а общую точку (рис. 6,6).
Аналогично в пространстве можно рассмотреть полупространства, ограниченные плоскостью.
Теорема 3. Плоскость разбивает пространство на два полупространства. Если точки А и В принадлежат одному полупространству, то отрезок АВ не пересекает плоскость. Если точки Аи В принадлежат разным полупространствам, то отрезок АВ пересекает плоскость.
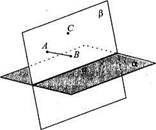
Доказательство. Пусть а — данная плоскость. Отметим точку С, не лежащую в плоскости (такая точка существует по аксиоме Cj). Разобьем все точки пространства следующим образом. Точку А отнесем к первому полупространству, если отрезок АС не пересекает плоскость а, и ко второму полупространству, если отрезок АС пересекает плоскость а. Покажем, что это разбиение пространства обладает свойствами, указанными в теореме.
Пусть точки А и В принадлежат первому полупространству. Проведем через точки С, Aw. В плоскость р. Если плоскость Р не пересекает плоскость а, то отрезок АВ тоже не пересекает эту плоскость. Допустим, что плоскость Р пересекает плоскость а (рис. 7, о). Так как плоскости различны, то их пересечение происходит по некоторой прямой а. Прямая а разбивает плоскость Р на две полуплоскости. Точки А и В принадлежат одной полуплоскости, именно той, в которой лежит точка С. Поэтому отрезок АВ не пересекает прямую а, а значит, и плоскость а.
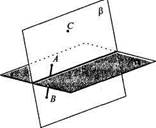
Если точки Аи В принадлежат второму полупространству, то плоскость р заведомо пересекает плоскость а, так как отрезок АС пересекает плоскость а. Точки A vs. В принадлежат одной полуплоскости разбиения плоскости Р прямой а. Следовательно, отрезок АВ не пересекает прямую а, а значит, и плоскость а.
|
|
| а) |
| б) |
Если, наконец, точка А принадлежит одному полупространству, а точка В — другому, то плоскость Р пересекает плоскость а, а точки А и В лежат в разных полуплоскостях плоскости р относительно прямой а (рис. 7, б). Поэтому отрезок АВ пересекает прямую а, а значит, и плоскость а. Теорема доказана.
Вопросы и задания
1. Сформулируйте основное свойство расположения точек относительно прямой в
плоскости.
2. Сформулируйте основное свойство расположения точек относительно плоскости
в пространстве.
3. Точки А и В относительно плоскости а принадлежат одному полупространству.
Отрезки АЙГ, ВК не пересекают плоскость а. К какому полупространству
принадлежит точка 1С?
4.Какой фигурой может быть пересечение:
1) полупространства и прямой;
2) полупространства и луча;
3) полупространства и плоскости;
4) полупространства и полуплоскости;
5) полупространства и отрезка;
Задачи
1.Точка А принадлежит плоскости a, a
точка В не принадлежит. Принадлежит ли
плоскости а середина отрезка АВ?
2.Отрезки АВ и АС пересекают плоскость а. Пересечет ли ее отрезок
ВС? А прямая ВС?
3.В плоскости а даны две пересекающиеся прямые а и Ъ. Mia.
Постройте линию пересечения плоскостей, проходящих через а и
М, через ЬиМ.
4.Дано: ccnp =m, Ае a, Be т, АфВ. Правильно ли: 1) (АВ) с а;
2) (АВ) <2 Р
Date: 2015-04-23; view: 3689; Нарушение авторских прав