Если две параллельные плоскости пересекаются третьей, то линии их пересечения параллельны

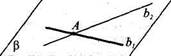
Доказательство. Пусть аир — параллельные плоскости, у — секущая плоскость, а и Ь — линии пересечения (рис. 16). Докажем, что прямые а и Ъ параллельны.

Предположим, что а и Ъ не парал­лельны. Тогда, так как они лежат в одной плоскости у, то пересекутся в некоторой точке Р. Точка Р принадлежит прямым а и Ъ и, значит, является общей точкой плос­костей аир. Но это противоречит тому, что плоскости а и Р параллельны. Итак,

прямые а и & не пересекаются. Значит, они параллельны. Теорема доказана.

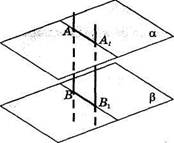
Теорема 10. Отрезки параллель­ных прямых, заключенные между двумя параллельными плоскостями, равны.

Рис. 17

Доказательство. Пусть отрез­ки АВ и А₁В₁ параллельны, а их концы лежат в параллельных плоскостях а и р (рис. 17). Третья плоскость, проходящая через прямые АВ и A_XB_V пересекает параллельные плоскости аир по параллельным прямым: (AAJ || (BBJ. Кроме того, по условию теоремы (АВ) || (AjSj). Значит, четырехугольник АВВ₁А₁ — параллелограмм. Следовательно, \АВ\ = \А_ХВ^. Теорема доказана.

Теорема 11. Через точку вне данной плоскости можно провести плоскость, параллельную данной, и притом только одну.

Рис.18

Доказательство. Пусть а — плоскость, А — не лежащая на ней точ­ка. Чтобы через данную точку А про­вести плоскость р, параллельную плос­кости а, сначала в плоскости а прове­дем какие-нибудь две пересекающиеся прямые а_х и а₂ (рис.18). Потом через данную точку А проведем параллельные им прямые &_х и Ь₂. Прямые &_х и Ъ₂ определяют единственную плоскость р (теорема 2). А по следствию теоремы 8 Pilot. Единственность такой плоскости Р не вызывает сомнений.

Следствие. Две плоскости, параллельные третьей плоскости, параллельны.

Следствие легко доказывается с помощью теоремы 11. Если даны три плоскости а, р, у, такие, что а || у, Р || у, то ясно, что Р || а. Действительно, если предположим, что а п р = Ъ (прямая), то через некоторую точку А прямой Ъ проходили бы две плоскости, парал­лельные плоскости у. А это противоречит теореме 11. Поэтому а || р.

Вопросы и задания

1. Какие плоскости называются параллельными?

2. Докажите теорему о признаке параллельности двух плоскостей.

3. Докажите, что если две параллельные плоскости пересекаются третьей, то
прямые пересечения параллельны.

4. Докажите, что отрезки параллельных прямых, заключенные между двумя
параллельными плоскостями, равны.

5. Докажите, что через точку вне данной плоскости можно провести плоскость,
параллельную данной, и притом только одну.

6. Повторите и запомните следствия теорем.

7. В окружающей вас обстановке найдите примеры параллельных плоскостей,
плоскости и параллельной ей прямой.

Задачи

49.Две прямые плоскости а параллельны плоскости р. Следует ли
отсюда, что а || р?

50.а || р. Докажите, что каждая прямая плоскости а параллельна
плоскости р.

51.Отрезки О А, ОВ и ОС не лежат в одной плоскости. Докажите,
что плоскость, проходящая через их середины, параллельна плос­
кости ABC.

52.Могут ли быть равными отрез­
ки не параллельных прямых,
заключенные между двумя
параллельными прямыми?

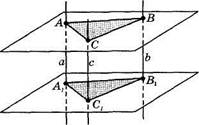
53.Через вершины треугольни­
ка ABC, лежащего в одной из
двух параллельных плоскос­
тей, проведены параллельные
прямые, пересекающие вторую
плоскость в точках A_VB_VC_V
Докажите равенство треуголь­
ников ABC и А₁В₁С₁ (рис.19).

В

54. Две параллельные плоскости аир пересекают сторону АВ тре­
угольника ABC в точках D и D_x, а сторону ВС соответственно в
точках Е и Е_х Найдите длину отрезка DE, если \BD\ = 12 см,
\BD_X\ = 18 см, l-Dj-EJ = 54 см.

55. Плоскость у пересекает плоскости а и р по параллельным пря­
мым. Следует ли из этого, что плоскости аир параллельны?

56. Плоскости аир пересекаются. Докажите, что любая плоскость
пространства пересекает хотя бы одну из плоскостей а, р.

Через вершины параллелограмма ABCD, лежащего в одной из
двух параллельных плоскостей, проведены параллельные прямые,
пересекающие вторую плоскость в точках A₁,B₁,C₁,D₁. Докажите,
что четырехугольник A₁,B₁,C₁,D₁ тоже параллелограмм.

58. Прямая а параллельна плоскости а.
Как через прямую а провести плос­
кость, параллельную а?

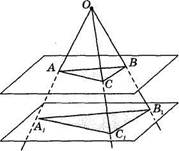
59. Три прямые, проходящие через
одну точку, пересекают данную
плоскость в точках А, В, С, а парал­
лельную ей плоскость в точках A_v B_v
C_v Докажите подобие треугольников
ABC и A^q (рис. 20).

60. ABCDEFA — не плоская

Рис. 20

замкнутая ломаная из шести звеньев.

Докажите, что если [АВ] || [DE], [ВС] \\ [EF] и [CD] || [FA], то \АВ\ = \DE\, \ВС\ = \EF\ и |СД = \FA\. 61. Докажите, что если прямая пересекает одну из двух параллельных плоскостей, то пересекает и другую.

Date: 2015-04-23; view: 3478; Нарушение авторских прав