Сечения

Способы задания плоскости и параллельного проектирования часто используют при построении сечений многогранников. Определение многогранника мы дадим в 11 классе. Пока ограничимся двумя простейшими примерами многогранников: прямоугольным паралле­лепипедом и тетраэдром.

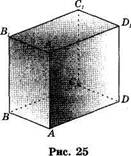
Прямоугольный параллелепипед имеет 6 гра­ней, 12 ребер, 8 вершин (рис. 25). Все его гра­ни — прямоугольники. Один из видов прямо­угольного параллелепипеда — куб. Все грани куба—равные квадраты. Когда говорят "парал­лелепипед ABCD Afifi^D", имеют в виду, что его основание ABCD, а боковые ребра AA_V BB_V CC DD

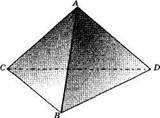
Тетраэдр (треугольная пирамида) имеет 4 грани, 6 ребер, 4 вершины (рис.26). Каждая грань тетраэдра — треугольник. Если все ребра тетраэдра равны, его называют правильным тетраэдром.

Таким образом, что такое сечение мно­гогранника?

Если, по крайней мере, две точки мно­гогранника лежат по разные стороны от плоскости, то говорят, что плоскость пересе­кает многогранник. В этом случае ее назы­вают секущей плоскостью. Фигура, состоя­щая из всех точек, общих для многогранника и секущей плоскости, называется сечением многогранника данной плоскостью.

На рисунке 27 изображены тетраэдр ABCD и секущая плоскость р. Точки Аи В лежат по разные стороны от секущей плоскости. Четырехугольник LMNK — сечение данного тетраэдра плоскостью |3.

Чтобы построить сечение многогранника плоскостью, надо задать эту плоскость: указать три (не лежащие на одной прямой) точки, через которые проходит эта плоскость, или точку и прямую и т.д.

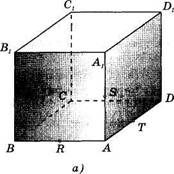
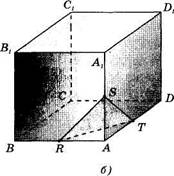
Пример. Постройте сечение куба ABCDA_lB₁C₁D₁ плоскостью, проходящей через точки R,S,T — середины ребер АВ, AA_lf AD (рис. 28, а).

Решение. Точки R, S, Т не лежат на одной прямой, поэтому задают некоторую плоскость. Требуется на данном изображении куба построить изображение указанного сечения. Точки А и S лежат в плоскости грани АВВ₁А₁ куба и в секущей плоскости. Значит, эти плоскости пересекаются по прямой AS. Секущая плоскость пересекает квадрат АВВ₁А₁ по отрезку AS. Аналогично убеждаемся, что две другие грани куба секущая плоскость пересекает по отрезкам ST, RT. Построив их, получим треугольник RST. Это и есть искомое сечение (рис. 28, б).

Вопросы и задания

1. Как получить параллельную проекцию: а) точки; б) фигуры?

2. Какая фигура является параллельной проекцией: а) отрезка; б) прямой?

3. Какие свойства фигур сохраняются при параллельном проектировании?
А какие не сохраняются?

4. Приведите реальные примеры проектирования.
5**. Докажите теорему о проекциях отрезков.

Задачи

62. Отрезок а — проекция отрезка Ъ. Всегда ли отрезок а короче Ь?

63. Может ли ромб быть проекцией квадрата? А трапеции?

64. Существует ли неплоская фигура, проекция которой — отрезок?

65. Треугольник AJZfi^ — проекция треугольника ABC. Постройте
проекции средних линий треугольника ABC.

66. Треугольник А₁В₁С₁ — проекция треугольника ABC. Постройте
проекции медиан треугольника ABC.

67. Может ли сечением куба быть треугольник, правильный треуголь­
ник, прямоугольник, квадрат, трапеция?

68. Точка К — середина ребра AD тетраэдра ABCD. Постройте сече­
ние тетраэдра плоскостью, проходящей через точки В, С и К.

В

69. Может ли неравнобедренная
трапеция быть проекцией равно­
бедренной трапеции? А наоборот?

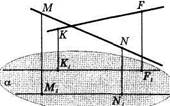
70. Пересекаются ли прямые MN и
KF, изображенные на рисунке 29, если
M₁N₁ и K₁F₁ — их проекции на
плоскость а?

71. Нарисуйте произвольную трапе­
цию AjBjCjDj Пусть она — проекция
некоторой равнобедренной трапеции

ABCD. Постройте проекцию высоты этой трапеции, проведенной из вершины В.

72.ТочкаМ — середина ребра CD тетраэдра ABCD. Постройте сече­
ние тетраэдра плоскостью, проходящей через прямую АВ и
точку М.

73.Точки К, Р, Т — середины трех ребер, выходящих из одной
вершины тетраэдра. Построить сечение тетраэдра плоскостью,
проходящей через точки К, Р, Т.

77. Четырехугольник A₁B₁C₁D₁ — проекция параллелограмма ABCD.
Если: 1) \АА_Х\ = 2 м, |BB_t| = 3 м, \СС_г\ = 8 м;

2) |AAj| = a, IBBJ = Ъ, \СС_г\ = с, то найдите длину отрезка DD_V

Date: 2015-04-23; view: 2036; Нарушение авторских прав