Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Простейшие следствия аксиом
|
|
Можно рассмотреть следствия, прямо вытекающие из аксиом. Их мы сформулируем в виде теорем.
Теорема 1. Через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну.
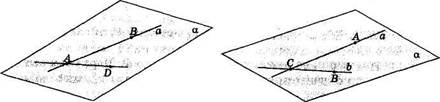
Доказательство. Пусть даны прямая а и не лежащая на ней точка D (рис. 4). Отметим на прямой а любые две точки: А и Б. Через точки А, В, D проведем плоскость и обозначим ее через а. По аксиоме С2 такую плоскость провести можно.
Докажем теперь, что плоскость а, проходящая через прямую а и точку D, единственна. Допустим, что существует другая, отличная от а, плоскость р, проходящая через прямую а и точку D. В этом случае по аксиоме С4 плоскости аир, будучи различными, пересекутся по прямой, и точки А, В, D должны будут лежать на этой прямой. Но по условию эти точки не лежат на одной прямой. Таким образом мы пришли к противоречию. Полученное противоречие и доказывает единственность плоскости. Теорема доказана.
Теорема 2. Через две пересекающиеся прямые можно провести плоскость, и притом только одну.
Доказательство. Пусть даны прямые о и 6, пересекающиеся в точке С (рис. 5). Обозначим любую точку на прямой а буквой А, на прямой b буквой В, отличные от С. По аксиоме С2 через точки А, В, С можно провести плоскость, и притом только одну. Теорема доказана.
Из аксиомы С2 и доказанных теорем следует, что плоскость можно задать: 1) тремя точками, не лежащими на одной прямой; 2) прямой и не лежащей на ней точкой; 3) двумя пересекающимися прямыми. Задание плоскости двумя параллельными прямыми рассмотрим в §4.
Вопросы и задания
1. Вспомните и повторите аксиомы планиметрии.
2. Даны две пересекающиеся прямые. Докажите, что эти прямые и пересекающая
их в различных точках третья прямая лежат в одной плоскости.
3. Докажите, что через прямую и не лежащую на ней точку можно провести плос
кость, и притом только одну.
4. Докажите, что через две пересекающиеся прямые можно провести плоскость, и
притом только одну.
Задачи
1. Можно ли через точку пересечения двух данных прямых провести
третью прямую, не лежащую с ними в одной плоскости? Объясните ответ.
2. Точки М, N, К лежат в каждой из двух различных плоскостей.
Докажите, что эти точки лежат на одной прямой.
3. Всегда ли прямая, которая пересекает две стороны треугольника
(не проходящая через его вершины), лежит в плоскости треугольника? Объясните ответ.
4. Всегда ли прямая, проходящая через вершину треугольника, лежит
в плоскости треугольника? Объясните ответ.
5. Четыре точки не лежат в одной плоскости. Могут ли какие-нибудь
три из них лежать на одной прямой? Объясните ответ.
в
6. Докажите, что через одну прямую можно провести две различные
плоскости.
7. Даны три точки, не лежащие на одной прямой. Через каждые две
из них проведены прямые. Докажите, что эти прямые лежат в одной плоскости.
8. Даны прямая а и точка А. Аеа. Докажите, что все прямые,
пересекающие прямую и проходящие через точку А, лежат в одной плоскости.
9. Даны две плоскости, пересекающиеся по прямой а. Прямая Ъ лежит
в одной из них и пересекается с другой. Докажите, что прямые а и Ъ пересекаются.
10. Точки А, В, С и D не лежат в одной плоскости. Пересекаются ли
прямые АС и BD?
11. Даны две не пересекающиеся плоскости. Докажите, что прямая,
пересекающая одну из этих плоскостей, пересекает и другую.
12. Докажите, что если прямые АВ и CD не лежат в одной плоскости,
то прямые АС и BD также не лежат в одной плоскости.
13. Четыре точки не лежат в одной плоскости. Сколько плоскостей
можно провести через три из них? Объясните ответ.
Date: 2015-04-23; view: 2391; Нарушение авторских прав