Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Аксиомы стереометрии
|
|
Глава I. АКСИОМЫ СТЕРЕОМЕТРИИ И ИХ ПРОСТЕЙШИЕ
СЛЕДСТВИЯ
АКСИОМЫ СТЕРЕОМЕТРИИ
В разделе планиметрии элементарной геометрии вы изучали свойства геометрических фигур, лежащих в одной плоскости. Теперь мы приступаем к изучению свойств фигур, у которых не все точки лежат в одной плоскости, т.е. фигур пространства. Эта часть геометрии называется стереометрией.
Стереометрия (от греч. stereos — пространственный и metreo — измеряю)—раздел геометрии, исследующий свойства пространственных фигур. В стереометрии рассматриваются математические модели тех материальных объектов, с которыми ежедневно имеют, дело архитекторы, конструкторы, строители и другие специалисты. Кроме того, школьный курс стереометрии служит основой черчения и начертательной геометрии — важнейших дисциплин любого технического вуза, поэтому этот раздел геометрии необходим всем.
Основными фигурами в пространстве являются точка, прямая и плоскость. Они принимаются без определений.
Как вы помните, в планиметрии рассматривалась только одна плоскость, и все изучаемые фигуры располагались в этой единственной плоскости. В стереометрии же приходится различать много плоскостей. Будем считать, что законы планиметрии распространяются на каждую плоскость.
Материальными моделями части плоскости являются, например, поверхность оконного стекла, хорошо отполированного пола и т.п. (рис. 1,а). Понятно, что это грубые модели. В геометрии плоскость мыслится неограниченной, идеально ровной и гладкой, не имеющей толщины.
Изображают плоскости в виде параллелограммов или других ограниченных частей плоскости (рис. 1,б,в). Обозначают их обычно греческими буквами а, р, у, 5 и др. Точки же и прямые отмечают так же, как в планиметрии.
Введение нового геометрического образа — плоскости—заставляет расширить систему аксиом. Поэтому мы вводим группу аксиом С, которая выражает основные свойства плоскостей в пространстве. Эта группа состоит из следующих аксиом.
Сг Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.
На рисунке 2,а точки А и В принадлежат плоскости а, а точки Е, F, К не принадлежат этой плоскости.
С2. Через любые три точки, не принадлежащие одной прямой, можно провести плоскость, и притом только одну.
На рисунке 2,6 изображена плоскость ос, проходящая через точки А, В, С. Эти точки не принадлежат одной прямой.
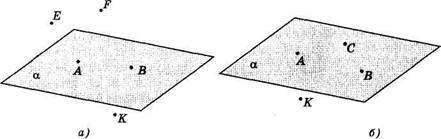
Рис. 2
С3. Если две точки прямой лежат в плоскости, то и вся прямая лежит в этой плоскости.
На рисунке 3,а и точка А и точка В прямой а принадлежат плоскости р (Ае р, Бе Р), поэтому сама прямая а лежит в плоскости значит (АВ) =ае
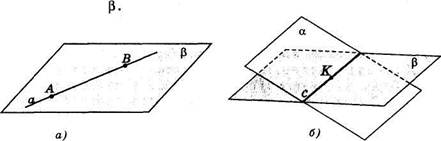
Рис. 3
С4. Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.
Как сказано в аксиоме, плоскости а и Р имеют общую точку, т.е. точку К (рис. 3,6). Точка ^принадлежит и плоскости ос, и плоскости р. Следовательно, обе рассматриваемые плоскости пересекаются по прямой. Это прямая с, которая проходит через точку К. Таким образом, ОЖУГвмя аксиом стереометрии состоит из аксиом планиметрии и аксиом V ( ,(\,(\,(\. Аксиомы планиметрии вам известны с 9-го класса.
В планиметрии мы и моли одну плоскость, на которой располагались все рассматривномыо нами фигуры, а в стереометрии много плоскостей. Поэтому мы должны учесть, что на любой плоскости, как бы она ни была расположена в пространстве, выполняются все планиметрические аксиомы.
Вопросы и задания
1. Что изучает стереометрия?
2. Сформулируйте аксиомы группы С.
3. Исходя из нижеследующих данных, объясните и изобразите, как расположены
точки, прямые и плоскости:
а)Аеа, Весе, Ceot, Dta; б) Ъ <z а, Ъ с Р;
e)anb = M, ana=N, Keanfi.
4с. Напишите следующие предложения в виде символов. В пространстве:
1)точка М принадлежит плоскости а, но не принадлежит плоскости Р;
2)прямая I и точка N, не лежащая на прямой Z, принадлежат плоскости р.
5. Известно, что оп6=М, иопо. Можно ли сказать, что а)Меа; б) be а?
6. Даны четыре точки, которые не лежат в одной плоскости. Докажите, что хотя
бы одна тройка точек не лежит на одной прямой.
7. Можно ли через: 1) три точки; 2) четыре точки, лежащие на одной прямой,
провести плоскость? Сколько плоскостей можно провести?
Date: 2015-04-23; view: 2402; Нарушение авторских прав