Собственные векторы и собственные значения

Рассмотрим 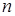-мерные векторы 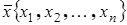и 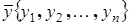, координаты которых связаны зависимостью

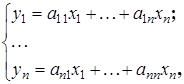(21.1)

где - любые скаляры. Тогда говорят, что вектору ставится в соответствие вектор 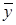по закону (21.1). Или: 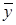есть образ . Так как в формулах (21.1) координаты 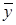выражены через координаты линейно и однородно, то это линейное преобразование вектора в вектор 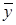с матрицей преобразования 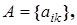где .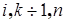

В матричной форме это преобразование принимает вид

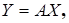(21.2)

где .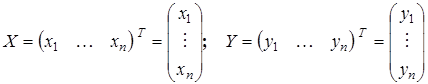

Определение 21.1: Закон вида (21.1), задающий линейное преобразование любого вектора 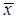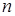-мерного арифметического пространства в некоторый вектор 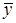этого же пространства называется линейным преобразованием.

Пример 21.1. Пусть задана матрица линейного преобразования 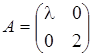, где 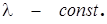Возьмем произвольный вектор 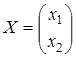и найдем образ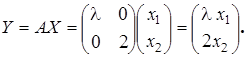

Если 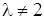, то вектор 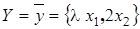. Следовательно, вектор изменит и длину и направление. Если 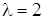, то вектор 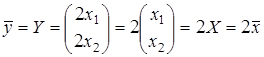, а это значит, что изменит только длину.

Рассмотрим преобразование 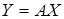с заданной матрицей 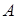. Будем искать такой вектор 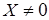, который в результате линейного преобразования меняет длину, но не меняет направление исходного вектора, т.е. 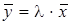или, в матричной форме,

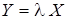. (21.3)

Тогда, подставив (21.3) в (21.2), имеем матричное уравнение

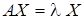(21.4)

Определение 20.2: ненулевой вектор 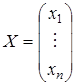называется собственным вектором матрицы 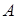, если выполнено равенство (21.4) 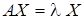, где 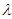- некоторое число. При этом 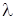называется собственным значением матицы .

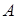Для нахождения собственного вектора 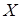решим уравнение (21.4).

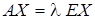, т.к. 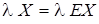, где 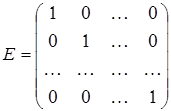- единичная матрица, играющая роль единицы в матричном исчислении. Тогда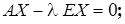

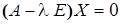. (21.5)

Получили однородную систему 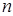линейных уравнений относительно неизвестных координат 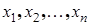собственного вектора 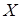с квадратной матрицей 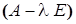. Матрица 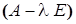имеет вид матрицы 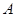, у которой из элементов главной диагонали вычли число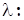

Необходимым и достаточным условием существования ненулевого решения такой системы является равенство нулю определителя матрицы этой системы, то есть

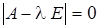. (21.6)

Если вычислить определитель этой матрицы, то он будет зависеть от 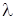и представлять собой многочлен степени 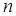. Его называют характеристическим многочленом, а равенство (21.6) – характеристическим уравнением. Решая уравнение (21.6), находят собственные значения 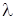. Для матрицы второго порядка 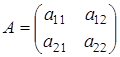характеристическое уравнение имеет вид , то есть вид квадратного уравнения относительно неизвестного собственного значения .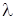

Пример 21.1. Зададимся матрицей преобразования 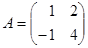и найдем собственный вектор 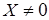, удовлетворяющий условию 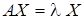. Для этого решим однородную систему (21.5):

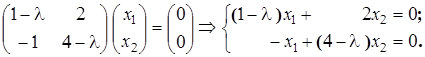(21.7)

Эта система имеет ненулевое решение, если ее определитель равен нулю, т.е. 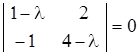. Вычислим характеристический многочлен

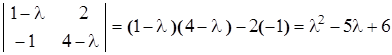
и для нахождения собственных значений приравняем его к нулю.

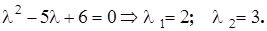
Найдем собственный вектор при 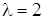. Подставим собственное значение 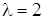в (21.7). Система примет вид:

.

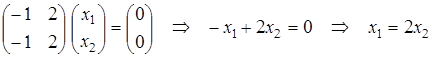Пусть . Тогда собственный вектор имеет вид .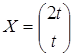

При 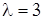система (21.7) имеет матричный вид 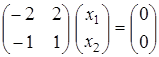, а, следовательно, можно записать, что 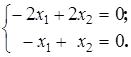Решение получается в базисной форме 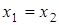и, полагая 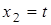, найдем собственный вектор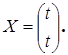

Рекомендуемая литература

1. Клиот - Дашинский М.И. Алгебра матриц и векторов. СПб.: Издательство «Лань», 1998.

2. Клиот-Дашинский М.И. Линейная алгебра. Методические указания к выполнению самостоятельной работы для студентов I курса. Л.: ЛИСИ, 1988.

3. Боревич З.И. Определители и матрицы. М.: «Наука», 1988.

4. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. Ростов-на-Дону: «Феникс», 1997.

Содержание

1. Определители второго порядка…………………………………………………….…..……3

2. Определители третьего порядка………………………………………………………………3

3.Элементарные сведения о перестановках……………………………………………………...5

4.Определители n-го порядка…………………………………………………...……………6

5. Основные свойства определителей……………………………………………………………7

6. Миноры и алгебраические дополнения элементов оп­ределителя………………………...8

7. Разложение определителей по элементам его рядов……………………………….……9

8. Общие сведения о матрицах. Основные определения…………………..……………..12

9. Разновидности матриц……………………………………………………………………..13

10. Арифметические операции над матрицами……………………………..…..…………15

11. Свойства перемножения матриц…………………………………………...…………...16

12. Обратная матрица и ее вычисление с помощью союзной матрицы……….……….18

13. Cистемы линейных уравнений………………………………………………………….....…20

14. Матричная запись системы уравнений………………………………………...……..……...21

15. Системы с неособенной квадратной матрицей. Формулы Крамера………………….........22

16. Системы уравнений в базисной форме…………………..…………………….………24

17. Метод Гаусса………………………………………………………………………………….26

18. Нахождение решения в базисной форме……………………………………….…..…..32

19. Вычисление обратной матрицы по схеме Гаусса………………………….…………….….33

20. Понятие об 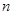-мерном арифметическом пространстве и 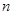-мерном векторе…………………………………………………………………………………………...…35

21. Линейное преобразование векторов. Собственные векторы и собственные значения…………………………………………………………………………………………….37

Лидия Евсеевна Морозова

Ольга Валентиновна Соловьева

Date: 2015-04-23; view: 782; Нарушение авторских прав