Обратная матрица и ее вычисление с помощью союзной матрицы

Определение 12.1. Пусть A - квадратная неособенная матрица.

Матрица называется обратной матрице A, если ее произведение на матрицу A и справа и слева равно единичной матрице E.

Обратную матрицу будем обозначать .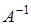

Таким образом 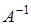- обратная для A, если .

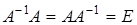Пусть A - неособенная матрица, т.е.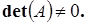

Составим вспомогательную матрицу H, состоящую из алгебраических дополнений элементов матрицы A:

.

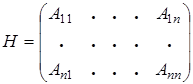Транспонируем матрицу H и получим матрицу C вида

.

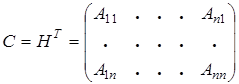Матрица C называется союзной матрицей.

Покажем, что .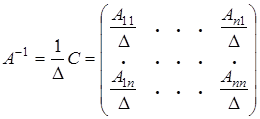

Доказательство:

По определению .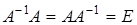

Рассмотрим элемент

(по теореме разложения и теореме аннулирования)

= .

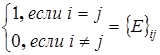Покажем, что матрица 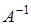- единственна. От противного: пусть существует матрица 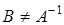такая, что 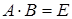. Умножим это равенство слева на .

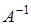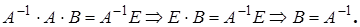
Получено противоречие, а значит матрица 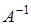- единственна. Таким образом, доказана теорема 12.1.

Для любой невырожденной матрицы A существует единственная обратная 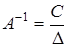, где С - союзная матрица.

Пример 12.1. Найти обратную матрицу для

.

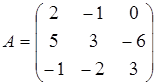Найдем определитель матрицы A:

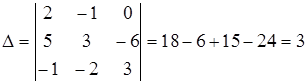
Найдем алгебраические дополнения элементов матрицы A:

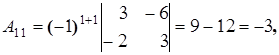
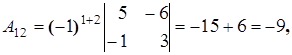
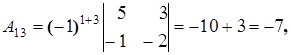
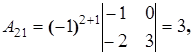
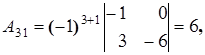
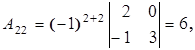
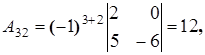
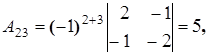
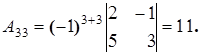
Составим союзную матрицу C:

,

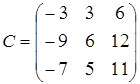тогда .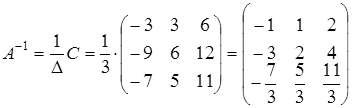

13. Cистемы линейных уравнений.

Рассмотрим систему m линейных уравнений с n неизвестными

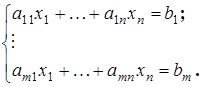(13.1)

Здесь - коэффициенты системы при неизвестных 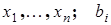- свободные члены или правые части системы.

Матрица 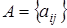, состоящая из коэффициентов системы, носит название матрицы системы. Если к матрице добавим столбец свободных членов, то получим расширенную матрицу

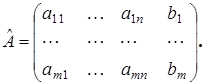
Матрицу - столбец свободных членов обозначим через В. Тогда 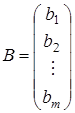. Если 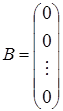, то система называется однородной.

Решением системы называется такая совокупность значений 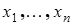, при подстановке которой в систему (13.1) все уравнения системы обращаются в тождество.

Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если решения системы не существует. Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если решений несколько.

Две системы с одним и тем же набором неизвестных называются равносильными в двух случаях: 1) каждое решение первой системы является решением второй, и наоборот; 2) обе системы несовместны. Равносильные системы должны иметь одинаковый набор неизвестных, но число уравнений может не совпадать.

14. Матричная запись системы уравнений.

Обозначим через X матрицу-столбец неизвестных

.

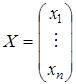Тогда

AX=B (14.1)

- матричная запись системы линейных уравнений (13.1). Если m = n, т.е. число уравнений равно числу неизвестных, то матрица А – квадратная. Для систем с квадратной неособенной матрицей можно искать решение в матричном виде. Умножим обе части матричного равенства (14.1) на 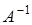слева:

,

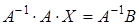и так как 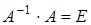и 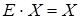, то получим решение системы в виде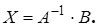

Пример 14.1: Используя найденную в примере 12.1 обратную матрицу, решить систему уравнений

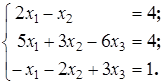
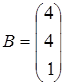Так как , а столбец свободных членов , то

Ответ: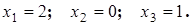

Date: 2015-04-23; view: 796; Нарушение авторских прав