Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Арифметические операции над матрицами
|
|
1. Сложение матриц. Складывать можно только матрицы одного размера.
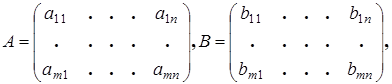
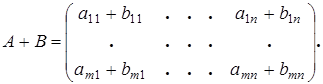
Пример 10.1: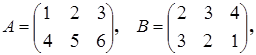 
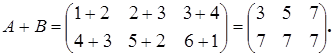
3) Умножение матриц на скаляр.
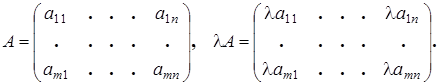
Пример 10.2: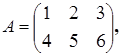 
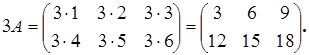
4) Умножение матриц.
Определение 10.1. Две матрицы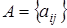 
размера 
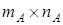и 
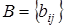размера 
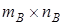называются соответственными, если число столбцов в 1-й матрице A равно числу строк во 2-й матрице B, т.е. 
.
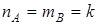Перемножать можно только соответственные матрицы A размера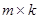 
и B размера 
.
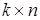Пусть A и B - соответственные матрицы.
Сформулируем правило умножения.
Произведением матрицы A на матрицу B называется матрица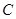 
, элементы которой вычисляются по формулам
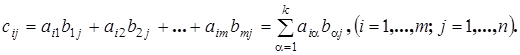
Здесь элементы i -й строки матрицы A попарно перемножаются с элементами j -го столбца матрицы B и складываются. В результате получается элемент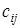 
произведения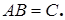 
Матрица C имеет размер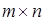 
.
Пример 10.3:
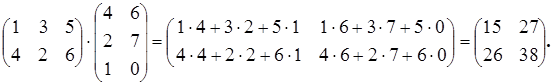
11. Свойства перемножения матриц .
1. Произведение матриц может равняться нулю при обоих множителях, отличных от нуля. Например:
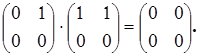
2. Произведение матриц в общем случае не коммутативно.
Проиллюстрируем этот результат на примерах. Рассмотрим следующие случаи:
а) A и B - соответственные, а B и A - не соответственные.
Например:
; 
.
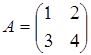Для таких матриц A и B произведение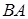 
не имеет смысла.
б) A и B -соответственные, B и A – соответственные.
; 
;
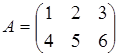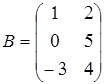AB: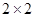 
; 
BA: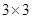 
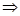AB и BA разных размеров и не могут сравниваться.
в) A и B - соответственные, B и A – соответственные и матрицы AB и BA одного размера, но AB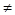 
BA. (A и B квадратные матрицы одного размера).
Пусть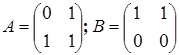 
. Тогда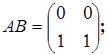 
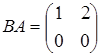. Следовательно,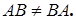 
3. Если матрицы A и B такие, что AB = BA, то говорят, что матрицы коммутируют друг с другом.
Рассмотрим случаи коммутативности квадратных матриц:
- скалярная матрица. Коммутирует с любой квадратной.
;
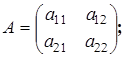
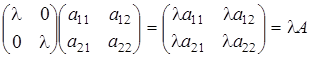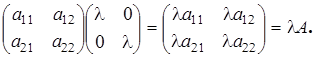
В частности, для единичной матрицы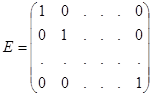 
: 
.
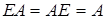Единичная матрица E в матричном исчислении играет ту же роль, что и единица в алгебре.
-диагональные матрицы коммутируют друг с другом.
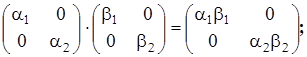
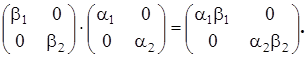
5) Остальные законы алгебры выполняются.
;
;
.
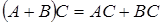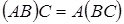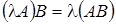Здесь A и B, A и С и B и C –соответственные матрицы;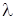 
- число.
6) Транспонирование произведения.
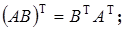
Действительно,
.
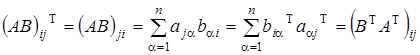7) Теорема 11.1.
Определитель произведения двух квадратных матриц n -го порядка равен произведению определителей перемножаемых матриц: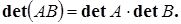 
.
Доказательство проведем на примере матриц 2-го порядка.
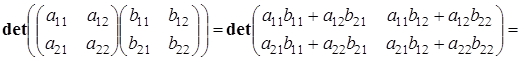
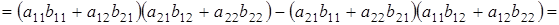
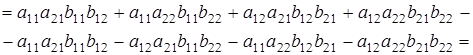
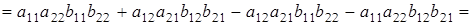
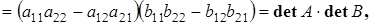что и требовалось доказать.
Date: 2015-04-23; view: 784; Нарушение авторских прав