Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Общие сведения о матрицах. Основные определения
|
|
Определение 8.1. Матрицей называется следующая прямоугольная таблица:
содержащая 
элементов 
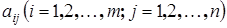, расположенных в т строках и в п столбцах.
Применяют также следующие обозначения матрицы: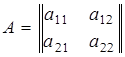 
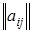, или 
, или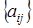 
.
Строки и столбцы матрицы именуются рядами.
Величина 
называется размером матрицы.
Если в матрице поменять местами строки и столбцы, то получим матрицу, называемую транспонированной. Матрица, транспонированная с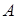 
, обычно обозначается символом 
.
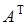Например: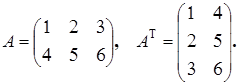 
Определение 8.2. Две матрицы A и B называются равными, если
1) обе матрицы одинаковых размеров, т.е.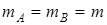 
и 
;
2) все их соответствующие элементы равны, т.е.
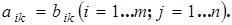(8.1)
Тогда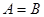 
. (8.2)
Здесь одно матричное равенство (8.2) эквивалентно скалярных равенств (8.1).
9. Разновидности матриц.
1) Матрица, все элементы которой равны нулю, называется ноль-матрицей:
2) Если матрица состоит только из одной строки, то она называется матрицей-строкой, например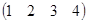 
. Аналогично этому матрица, имеющая только один столбец, именуется матрицей-столбцом, например 
.
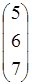Транспонирование переводит матрицу-столбец в матрицу-строку и наоборот.
3) Если m = n, то матрица называется квадратной матрицей n-го порядка.
Диагональ членов квадратной матрицы, идущая из левого верхнего угла в ее правый нижний угол, называется главной. Другая же диагональ ее членов, идущая из левого нижнего угла в ее правый верхний угол, именуется побочной.
Для квадратной матрицы может быть вычислен определитель det(A).
4) Если определитель матрицы равен нулю, то матрица называется особенной, или вырожденной. В противном случае матрица именуется неособенной, или невырожденной.
5) Разновидности квадратных матриц:
Если все элементы квадратной матрицы, за исключением элементов ее главной диагонали, равны нулю, то матрица называется диагональной. Диагональная матрица имеет вид: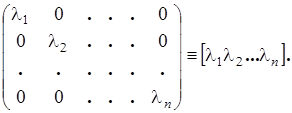 
Ее определитель равен произведению элементов главной диагонали: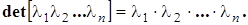 
В частности, при 
диагональная матрица называется скалярной: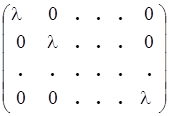 
. 
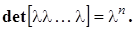
При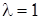 
скалярная матрица называется единичной и обозначается символом Е.
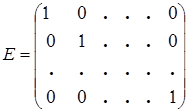. Ее определитель равен единице: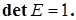 
Если все элементы квадратной матрицы по одну сторону главной диагонали равны нулю, то матрица именуется треугольной (соответственно верхней или нижней).
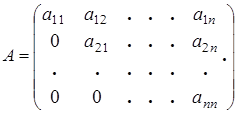- верхняя треугольная матрица.
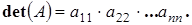
Date: 2015-04-23; view: 979; Нарушение авторских прав