Групи, підгрупи. Приклади. Найпростіші властивості груп

Алгебраїчна операція -це функція, що діє з декартового квадрату (АxА→А) в А(не порожня множина).АxА={(а,b),а є А, b є А}.

Внутрішня алгебраїчна операція завжди є необмежено виконана, однозначна та замкнена на мн.А. Результат дії операції прийнято позначати с=а f b або с=a*b.

Непорожня множина А, на якій задано хоча б одну алгебраїчну операцію, назив.алгебраїчною системою, та познач.: (А;*), де *-алгебраїчне позначення. Наприклад:групи, кільця, тіла..

Непорожня множина G на якій задана бінарна алгебраїчна операція(функція f, що діє з декартового добутку f:Р×А→А) назив. групою, якщо виконуються наступні умови:

1) для будь-яких a,b є G, існує і єдиний елемент с є G:[с=a*b]-замкненість;

2)для будь-яких a,b,с є G:[а*(b*с)=(а*b)*с]-асоціативність;

3)для будь-якого a є G існує e є G: [а*e=e*а=а]-існування нейтрального;

4) для будь-якого a є G існує х є G:[а*х=х*а=e]-існування симетричного.

Якщо крім цього виконується аксіома 5) для будь-яких a,b є G:[а*b=b*а],то група назив. комутативною або абелевою.

Групи, у яких «*» означає множення назив. мультиплікативною, а в яких «*» позначено додавання – адитивною.

Приклади: Адетивні гр. (Z;+),(Q;+),(R;+),(C;+).

Мультиплікативні абелеві гр. (Q\_{0};*), (R\_{0}; ·), (С\_{0};*). Загальна лінійна гр.(GLn(R); ·) в якій GLn(R)-множина не вироджених матриць n-го порядку над полем R; Р(х)-(поліном), М_m,n-(матриці) -групи. М_n – не група, особливі матриці обернених не мають, С[а,b] – не група,бо не всі функції мають обернені.

Найпростіші властивості груп:

1)Нейтральний елемент визначений в групі однозначно.

_▲Нехай е₁ і е₂ – нейтральні елементи.Покажемо, що е₁=е₂.Тоді для будь-якого а є G:а_*е₁ = =е_1*а=а; а_*е₂ = =е_2*а=а.Тоді е₂ = е_1* е₂= е_1▲

2)Кожний елемент групи має єдиний симетричний.

_▲Припустимо,що існує а є G:

а_*х₁=е і а_*х₂=е,(х₁ та х₂ – його симетричні).

х₁=х_1*е= х_1*(а_*х₂)=(х_1*а)_*х₂=е_*х₂=х₂ 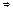х₁=х_2▲

3) Для будь-якого а є G обернений а^-1 тільки один.

_▲Нехай u і v-довільні обернені для а: аu=uа=е і аv=vа=е. u=uе=u(аv)=(uа)v=

=еv= v 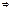u = v_▲

4) е^-1=е.

_▲Дійсно, е_*е=е 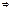е^-1=е _▲

5) (а^-1)^-1=а.

_▲Дійсно а^-1_*а=а_*а^-1=е 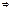(а^-1)^-1=а_▲

6) (аb)^-1= b^-1а^-1.

_▲Дійсно, (аb)(b^-1а^-1)=а(bb^-1)а^-1=аеа^-1=аа^-1=е. Аналогічно (b^-1а^-1)(аb)=е, значить(аb)^-1= b^-1а^-1_▲

Не порожня підмножина Н групи G називається підгрупою цієї групи, якщо Н є групою відносно операції визначеної на G.(Познач. Н≤ G)

Напр. (Q\_{0}; ٠)≤(R\_{0};٠)≤ ≤(С\_{0};٠), (2Ζ;+)≤(Ζ;+)? (SLn;٠)≤ (СLn;٠). Підгрупами будь-якої групи є одинична підгрупа Е і сама ця група. Критерій підгрупи:

Непорожня підмножина Н мультиплікативної групи G є її підгрупою тоді і тільки тоді,коли Н замкнена відносно«_*»елементів та взяття обернених елементів,т.б. Н містить добутки всіх своїх елементів і містить обернені до всіх своїх елементів.

_▲ Необхідність. Нехай Н< G,покажемо виконання умов:

Н₁: для будь-яких а, b є Н [аb є Н]

[а+b є Н]; Н₂: для будь-якого а є Н

[а^-1є Н] [-а є Н].Тоді Н сама є групою і за означенням групи

аb є Н(замкненість операції над Н),а^-1 є Н(існування обернених

е-тів).

Достатність. Якщо Н містить добутки своїх елементів і обернених до них, то виконуються аксіоми (1,4) групи.Асоціативність множення елементів у Н випливає із асоціативності множення у G. Якщо х є Н, то х^-1є Н і х_*х^-1=е=1 є Н. Отже, Н є групою._▲

Наслідок. Н є підгрупою G , коли виконується умова:для будь-яких х,у є Н [ху^-1 є Н].

Date: 2015-04-23; view: 1148; Нарушение авторских прав