Системы с неособенной квадратной матрицей. Формулы Крамера

Пусть система имеет неособенную матрицу, то есть 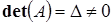. Систему уравнений (13.1) можно записать таким образом

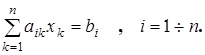(15.1)

Умножим обе части (15.1) на алгебраическое дополнение столбца номер j и просуммируем:

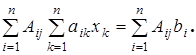(15.2)

Тогда левая часть (15.2) равна

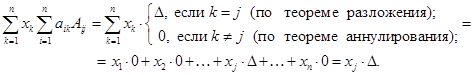
Правая часть равенства (15.2) на основании теоремы замещения равна тому определителю, который получается из исходного путем замены j -го столбца на столбец свободных членов. Обозначим его через 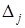. Тогда

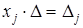, (15.3)

откуда получаем, что

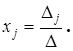(15.4)

Так как формулы (15.3) дают единственную совокупность решения, то решение системы (15.1) с квадратной невырожденной матрицей единственно. Таким образом, справедлива следующая теорема.

Теорема Крамера: если определитель 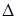системы с квадратной матрицей не равен нулю, то система имеет единственное решение, которое находим по формулам (15.4) для всех j = 1,2,…,n.

Пример 15.1: По формулам Крамера решить систему уравнений

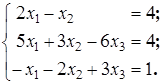
Решение: определитель матрицы системы 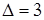(найден в примере 12.1).

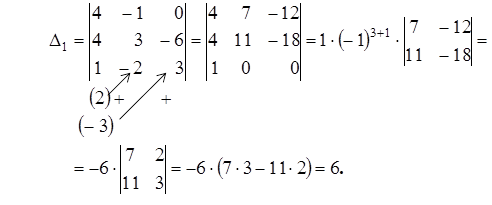
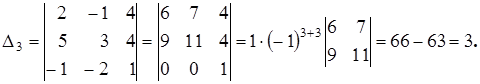
Тогда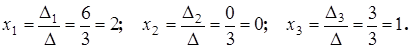

Ответ: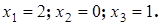

Из доказательства теоремы Крамера вытекает важное следствие для однородных систем с квадратной матрицей. Пусть в системе (15.1) все правые части равны 0. Тогда все определители 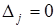, так как имеют нулевой столбец. Тогда из формулы (15.3) следует, что 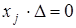для всех 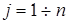. И если хотя бы одно значение в совокупности 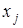отлично от 0 (то есть система имеет ненулевое решение), то это может быть только тогда, когда определитель системы 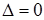. Заметим, что однородная система всегда имеет очевидное нулевое решение. О наличии других решений ответ дает следующая теорема.

Теорема: Для того, чтобы однородная система имела ненулевые решения, необходимо и достаточно равенство нулю ее определителя.

Формулы Крамера для нахождения решений применимы только для систем с квадратной матрицей и при больших значениях n приводят к трудоемкому процессу вычисления определителей высокого порядка.

Date: 2015-04-23; view: 747; Нарушение авторских прав