Другий критерій підкільця

Непорожня підмножина Н кільця К є його підкільцем 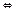, коли виконується умова:

а) для будь-яких х,у є Н [(х-у) є Н];

б) для будь-яких х,у є Н[ху є Н].

_▲Необхідність очевидна.

Доведемо достатність. Оскільки для будь-яких х,у є Н, (х-у) є Н,то з цього випливає:1) 0=х-х є Н; 2) -у=0-у є Н; 3) х+у=х-(-у) є Н.Таким чином «+» та «٠» замкнене на Н,Н містить 0 та протилежні до своїх елементів.Асоціативність,комутативність «+» та дистрибутивний закон виконується в Н,бо вони виконуються для всих елементів кільця К, Н-підкільце К._▲

Будь-яке кільце завжди містить принаймні 2 підкільця: {0} і {К}їх назив. тривіальними.

Т-ма. Перетин будь-якої множини підкілець кільця К є його підкільцем.

_▲Нехай К_і-підкільця кільця К,і єІ. Позначимо через А=∩ К_і.Перевіримо умови критерія: А≠ порожній множині, бо 0 є К_і(і є І).

1)Нехай х, у є А,тоді х,у є К_і (і є І). Оскільки К_і –підкільце,то (х-у) є К_і і ху є К_і (і є І).Отже,(х-у) є А і ху є А, т.б. А-підкільце._▲

Якщо К або асоціативне, або комутативне, або цілісне,то кожне його власне підкільце має аналогічну властивість. (унітарність може не зберігатись)

Приклад. К=Z; L=2Z.

Х арактеристикою кільця К з одиницею е назив. найменше натуральне число m=min{k/k є N}, таке що

m٠е=0.Якщо такого числа не існує, то характеристика кільця К дор.0, бо 0٠е=0.Позначення: char K.

Т-ма. Характеристикою будь-якого поля Р є або число 0,або просте число.

_▲Нехай характеристика поля Р дор. m.Припустимо, що m≠0 і m-складне число: m=р٠m₁,де р-просте число, m₁≥1.Покажемо, що m₁=1.Припустимо супротивне,тоді для одиниці е поля р виконується m٠е=0, р٠m₁٠е=(р٠е)(m₁٠е). Оскільки в полі немає дільників 0, то 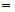m₁٠е=0, або р٠е=0.Остання рівність суперечить мінімальності вибору числа m, бо m₁<m,т.б. припущення не вірне m₁=1 і m=р.Таким чином характеристика поля є або 0 або просте число._▲

Ідеалом І кільця К назив. таке його підкільце,яке є замкнутим відносно множення на е-ти кільцяК

Розв’язком с-ми S назив. упорядкований набір чисел (α_1,…α_n), який є розв’язком усих р-нь с-ми, таким чином множина розв’язків с-ми є перетин множин розв’язків її рівнянь.Х_s=∩X_i (i=1,..,m).С-ма S назив. сумісною,якщо має розв’язки Х_s≠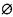

і несумісною,якщо не має розв’язків Х_s = 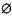, означена, якщо має тільки один розв’язок

Card X_s=1,неозначена,якщо має >1 розв’язку Card X_s >1.

А= 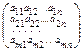-основна матриця с-ми,вона має розмір m×n(m-рядків,n-стовпців).

Ã= 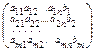-розширена матриця с-ми.

Мінор М_ij-це детермінант,який одержується з даного викреслюванням i-го рядка і j-го стовпця.Нехай матриця А має розмір m×n.Виберемо довільно к-рядків і к-стовпців,к≤ mіn(m,n). Елементи,що стоять на перетині вибраних рядків і стовпців утворюють матрицю к-го порядку, детермінант якої назив.мінором к-го порядку для даної матриці М(і₁,і₂,…,і_к; j₁,…, j_к).

Вектор -впорядкований набір n дійсних чисел. а=(α₁,…α_n), а-вектор, α₁,…,α_n-його компоненти. S=(а₁,а₂,…а_n)єRⁿ, а₁=(α₁₁,α₁₂…α_1n)……..

а_m=(α_m1,α_m2…α_mn),b=(β₁,..β_m)

якщо b=λ₁а₁+λ₂а₂+…+λ_mа_m, то вектор b назив.лінійною комбінацією даних векторів, λ₁,λ₂,…,λ_m-коефіцієнти комбінації.

Система векторів назив. лін.залежною, якщо існують такі коефіцієнти λ₁,λ₂,…,λ_n, серед яких хочаб один не дор.0, при яких лін. комбінація заданої с-ми векторів=нуль вектору.

С-ма векторів назив. лін.незалежною, якщо лін. комбінація цих векторів= =Ō і тоді і тільки тоді, коли всі коефіцієнти λ₁,λ₂,…,λ_n=0. Рангом ненульової с-ми назив. кількість векторів у будь-якому її базисі rang S. Лінійно незалежна с-ма твірних наз. базис або база даної с-ми Bas S.

Системою твірних с-ми векторів S назив. така підсистема Т через яку виражається вся с-ма.

Рангом ненульової с-ми є максимальна к-сть незалежних векторів в ній.

Date: 2015-04-23; view: 768; Нарушение авторских прав