Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать неотразимый комплимент
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Определители n-го порядка
Очевидно, что для системы из n линейных уравнений с n неизвестными получим матрицу коэффициентов размером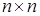 
:
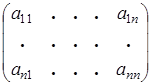
Введем понятие определителя n-го порядка.
Определение 4.1:
Определителем n-го порядка называется число равное
-сумме n! слагаемых;
-каждое слагаемое есть произведение n элементов матрицы, взятых по одному из каждой строки и каждого столбца;
-каждое слагаемое берется со знаком «+», если перестановка из вторых индексов четная, и со знаком «-», если перестановка из вторых индексов нечетная, при условии, что первые индексы образуют натуральный ряд чисел.
Т.о.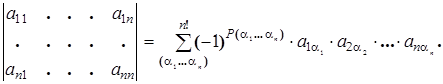 
Здесь å берется по всем возможным перестановкам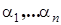 
, составленным из чисел 1,2,…,n.
5. Основные свойства определителей.
Установим основные свойства определителей, которые для простоты будем показывать на определителе 2-го порядка.
1. При замене строк соответствующими столбцами (именуемой транспонированием) определитель остается неизменным. Действительно:
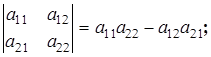
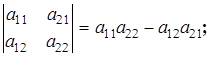
Следовательно, 
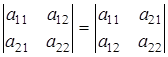, что и требовалось доказать.
Примечание: Полученный выше результат дает нам право утверждать, что строки и столбцы определителя, именуемые в дальнейшем рядами, равноправны.
2. При перестановке двух рядов определитель меняет знак на противоположный.
Действительно,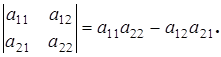 
Поменяем местами строки и вычислим определитель
,
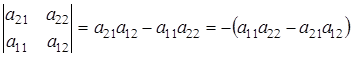что и требовалось доказать.
3. Если в определителе два параллельных ряда одинаковы, то он равен нулю. Действительно, поменяем местами две одинаковых строки. Тогда величина определителя не изменится, а знак в силу свойства 2. поменяется. Единственное число, которое не меняется при изменении знака – ноль.
4. Общий множитель членов любого ряда можно вынести за знак определителя.
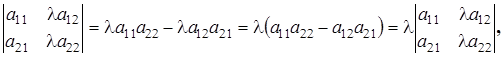что и требовалось доказать.
5. Если все элементы любого ряда являются суммами одинакового числа слагаемых, то определитель равен сумме определителей, в которых элементами рассматриваемого ряда служат отдельные слагаемые.
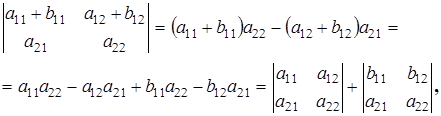
что и требовалось доказать.
6. Определитель не изменится, если к элементам любого ряда прибавить соответствующие элементы параллельного ряда, умноженные на некоторое число.
Умножим вторую строку на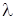 
и прибавим ее к первой строке:
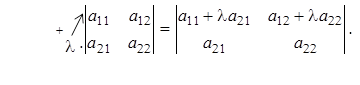
Действительно, в силу свойств 3,4,5
=
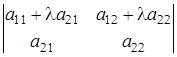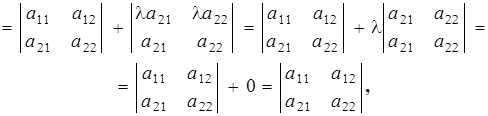
что и требовалось доказать.
6. Миноры и алгебраические дополнения элементов определителя.
Рассмотрим определитель n-го порядка:
.
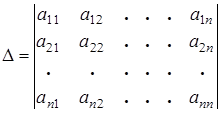Выделим в определителе 
i-ю строку и j-й столбец. На пересечении этих рядов стоит элемент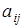 
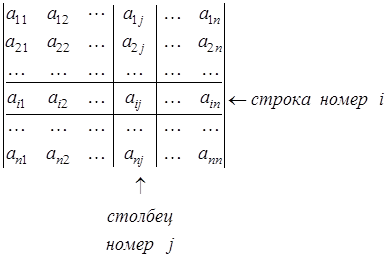
Если в определителе мы вычеркнем i-ю строку и j-й столбец, то получим определитель порядка п-1 (т. е. имеющий порядок, на единицу меньший по сравнению с исходным определителем), называемый минором элемента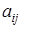 
определителя 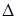. Будем обозначать минор элемента 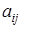символом 
.
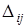Определение 6.1. Алгебраическим дополнением элемента 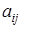определителя 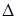называется минор 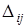, взятый со знаком 
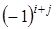, и обозначается символом 
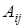. Согласно определению получим
.
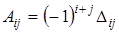Пример 6.1. Найти минор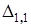 
и алгебраическое дополнение 
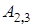определителя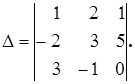 
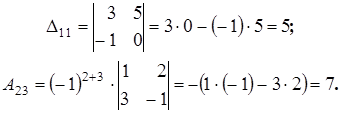
Date: 2015-04-23; view: 1002; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |