Разложение определителей по элементам его рядов

1.Теорема разложения:

Всякий определитель равен сумме парных произведений элементов какого-либо ряда на их алгебраические дополнения.

Для i- й строки:

;

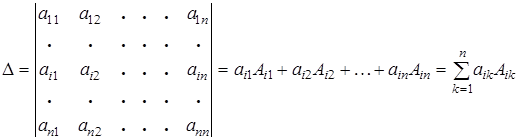или для j -го столбца:

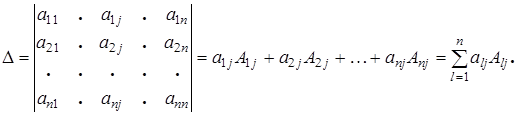
Пример 7.1. Вычислить определитель разложением по элементам первой строки:

=1∙(1+12+12 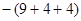) 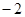∙(2+16+18 )+

+3∙(4+8+27 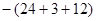) 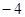∙(8+4+18 )=

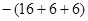=8 = .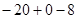

Теорема разложения позволяет заменить вычисление одного определителя n- го порядка вычислением n определителей (n- 1)-го порядка.

Однако для упрощения вычислений целесообразно для определителей высоких порядков использовать метод «размножения нулей», основанный на свойстве 6 раздела 5. Его идея:

-сначала «размножить нули» в некотором ряду, т.е. получить ряд, в котором только один элемент не равен нулю, остальные нули;

-затем разложить определитель по элементам этого ряда.

Следовательно, на основании теоремы разложения исходный определитель равен произведению ненулевого элемента на его алгебраическое дополнение.

Пример7.2. Вычислить определитель:

.

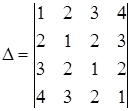«Размножим нули» в первом столбце.

От второй строки вычтем первую, умноженную на 2, от третьей строки вычтем первую, умноженную на 3, а от четвертой строки вычтем первую, умноженную на 4. При таких преобразованиях величина определителя не изменится.

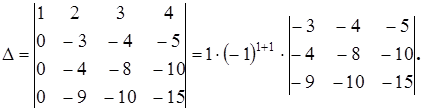
По свойству 4 раздела 5 можем вынести 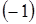за знак определителя из 1-го столбца, 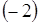из 2-го столбца и 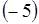из 3-го столбца.

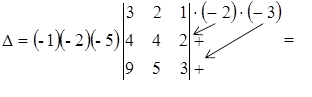
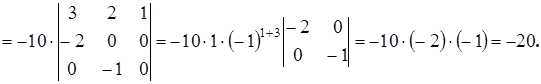
Следствие: Определитель с нулевым рядом равен нулю.

2. Теорема замещения:

Сумма парных произведений каких-либо чисел на алгебраические дополнения некоторого ряда определителя равна тому определителю, который получается из данного, если в нем заменить элементы этого ряда взятыми числами.

Для 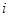-й строки:

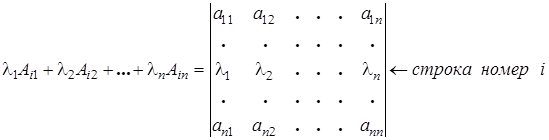
1. Теорема аннулирования:

Сумма парных произведений элементов какого-либо ряда на алгебраические дополнения параллельного ряда равна нулю.

.

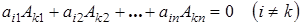Действительно, по теореме замещения получаем определитель, у которого в k -й строке стоят те же элементы, что и в i -й строке

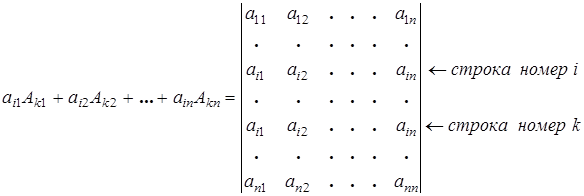
Но по свойству 3 раздела 5 такой определитель равен нулю.

Т.о., теорему разложения и ее следствия можно записать следующим образом:

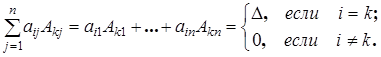
Date: 2015-04-23; view: 2414; Нарушение авторских прав