Линейные операторы в евклидовом пространстве

9.1. Какой оператор А * называется сопряженным к линейному оператору А в евклидовом пространстве? Будет ли он единственным? Как найти его матрицу, зная матрицу оператора

А в ортонормированном базисе?

9.2. Как найти оператор, сопряженный к произведению операторов АВ; к их сумме А+В? Чему равен сопряженный оператор к обратному оператору ?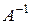

9.3. Какой оператор называется самосопряженным? Каково характеристическое свойство матрицы самосопряженного оператора в ортонормированном базисе? Сохраняется ли самосопряженность при сложении операторов; при умножении их на числа; при умножении операторов?

9.4. Какова специфика корней характеристического уравнения для самосопряженного оператора? Каковы свойства его собственных векторов?

9.5. Какой оператор называется ортогональным? Что происходит с ортонормированным базисом при действии ортогонального оператора?

9.6. Известно, что линейный оператор переводит ортонормированный базис в ортонормированный. Каков этот оператор?

9.7. Будет ли ортогональный оператор иметь обратный? Если да, то как его найти?

9.8. Известно, что оператор А обратим, и 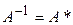. Каков этот оператор?

9.9. Каковы свойства матрицы ортогонального оператора в ортонормированном базисе?

9.10*. Как показать, что при переходе от одного ортонормированного базиса к другому ортонормированному базису матрица самосопряженного оператора преобразуется так же, как матрица соответствующей квадратичной формы? Для чего здесь нужна самосопряженность оператора?

Литература

1. Бугров Я. С., Никольский С. М. Дифференциальное и интегральное исчисление. – М.: Наука, 1980.

2. Головина Л. И. Линейная алгебра и некоторые ее приложения. – М.: Наука, 1985.

3. Линейная алгебра и основы математического анализа. Сборник задач по математике для втузов. Ред. Ефимов А. В., Демидович Б. П. – М.: Наука, 1986.

4. Рублев А. Н. Курс линейной алгебры и аналитической геометрии. – М.: Высшая школа, 1972.

СОДЕРЖАНИЕ

Теоретические вопросы……………………. 3

Date: 2015-04-23; view: 722; Нарушение авторских прав