Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Евклидовы пространства
|
|
8.1. Какие аксиомы определяют скалярное произведение в евклидовом пространстве? Что они означают на языке билинейных форм? Приведите примеры скалярных произведений.
8.2. Что такое матрица Грама? Каковы ее свойства? Как записать с ее помощью скалярное произведение векторов? Может ли матрица Грама в некотором базисе 
иметь вид: а) 
; б) 
; в)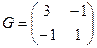 
?
При положительном ответе найти 
, где
.
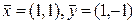8.3. Что такое длина (норма) вектора в евклидовом пространстве? Каковы ее свойства? Что такое неравенство Коши–Буняковского? Когда оно превращается в равенство? Как выглядит неравенство треугольника, и почему оно так называется?
8.4. Как вычисляется угол между векторами? Почему это определение угла корректно? Какие векторы называются ортогональными? Скалярное произведение в базисе 
задается матрицей Грама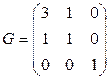 
. Будут ли ортогональны векторы 
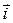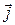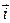и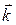 
; 
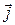и 
; и 
? Каковы длины векторов ?
8.5. Что такое ортогональный, ортонормированный базисы в евклидовом пространстве? Как выглядит матрица Грама в ортогональном базисе, в ортонормированном? Как ищется скалярное произведение в ортонормированном базисе? Почему? Как выражаются через скалярное произведение координаты вектора в ортонормированном базисе?
Date: 2015-04-23; view: 707; Нарушение авторских прав