
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Линейные операторы
|
|
6.1. Что такое линейный оператор? Привести примеры линейных операторов в пространствах  . Какой вектор сохраняется при действии любого линейного оператора?
. Какой вектор сохраняется при действии любого линейного оператора?
6.2. Какие из следующих отображений, действующих на геометрические векторы  , являются линейными операторами (векторы
, являются линейными операторами (векторы 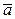 и
и 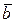 фиксированы):
фиксированы):
а)  ; б)
; б)  ;
;
в) 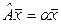 ; г)
; г) 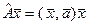 ;
;
д)  ; е)
; е) 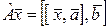 ;
;
ж) 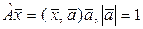 (каков геометрический смысл?);
(каков геометрический смысл?);
з) 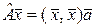 ; и)
; и) 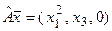 ;
;
к) 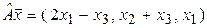 ; л)
; л)  ;
;
м) 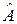 - поворот вокруг оси OZ на угол a;
- поворот вокруг оси OZ на угол a;
н) 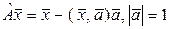 (каков геометрический смысл?).
(каков геометрический смысл?).
6.3. Какие из следующих отображений являются линейными операторами в пространстве L:
а) 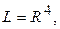

 ;
;
б) 
 ;
;
в) 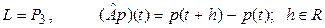 ;
;
г) 
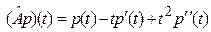
д) L=P – пространство всех многочленов (объяснить, почему это линейное пространство),
 ;
; 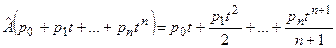
– интегрирование.
6.4. Что такое матрица линейного оператора в данном базисе? Как она изменится, если поменять местами два базисных вектора?
Пусть линейный оператор 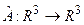 переводит векторы
переводит векторы 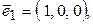
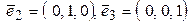 соответственно в векторы
соответственно в векторы 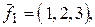

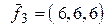 . Какова его матрица в базисе
. Какова его матрица в базисе 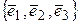 ?
?
6.5. Известна матрица оператора в некотором базисе. По какой формуле преобразуются координаты векторов под действием этого оператора?
6.6. Что такое сумма, произведение линейных операторов? Что происходит с матрицами линейных операторов при сложении, умножении операторов?
6.7. Как образуется матрица перехода от данного базиса к новой системе векторов? Каков критерий базисности новой системы? Как преобразуются координаты векторов и матрица линейного оператора при переходе к другому базису? Что происходит при этом с определителем матрицы?
6.8. Какие матрицы называются подобными? Какие свойства подобия матриц Вы знаете? Как связаны между собой определители подобных матриц? Ответ на последний вопрос обоснуйте.
6.9. Какой оператор называется невырожденным? Что такое обратный оператор? Каков критерий его существования? Как найти матрицу обратного оператора? Известно, что линейный оператор 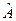 переводит вектор
переводит вектор 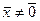 в нуль-вектор. Существует ли
в нуль-вектор. Существует ли 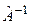 ? Ответ обосновать.
? Ответ обосновать.
6.10. Что такое собственный вектор линейного оператора? Каков геометрический смысл собственного вектора в пространстве 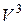 ? Пусть
? Пусть 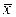 – собственный вектор. Укажите еще какой-нибудь собственный вектор, отвечающий тому же собственному значению. Ответ обосновать. Могут ли быть линейно зависимыми собственные векторы, отвечающие различным собственным значениям?
– собственный вектор. Укажите еще какой-нибудь собственный вектор, отвечающий тому же собственному значению. Ответ обосновать. Могут ли быть линейно зависимыми собственные векторы, отвечающие различным собственным значениям?
6.11. Верны ли утверждения:
а) если 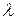 – собственное значение оператора
– собственное значение оператора 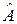 , то
, то  – собственное значение для оператора
– собственное значение для оператора  ;
;
б) если 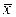 – собственный вектор операторов
– собственный вектор операторов 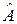 и
и 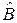 с собственными значениями
с собственными значениями  и
и  соответственно, то
соответственно, то 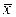 – собственный вектор для
– собственный вектор для 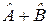 ; для
; для  ? Если да, то с каким собственным значением?
? Если да, то с каким собственным значением?
6.12*. Исходя из геометрического смысла оператора 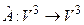 , указать его собственные значения и собственные векторы. Обладает ли он базисом из собственных векторов? Если да, то как выглядит матрица оператора в этом базисе? Является ли оператор невырожденным?
, указать его собственные значения и собственные векторы. Обладает ли он базисом из собственных векторов? Если да, то как выглядит матрица оператора в этом базисе? Является ли оператор невырожденным?
а) 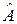 – оператор проектирования векторов на плоскость P;
– оператор проектирования векторов на плоскость P;
б) 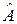 – оператор проектирования векторов на прямую L;
– оператор проектирования векторов на прямую L;
в) 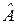 – оператор симметрии векторов относительно плоскости P;
– оператор симметрии векторов относительно плоскости P;
г) 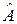 – оператор симметрии векторов относительно прямой L;
– оператор симметрии векторов относительно прямой L;
д) 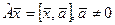 – фиксированный вектор.
– фиксированный вектор.
6.13. Что такое характеристический многочлен линейного оператора? Зачем он нужен? Как он зависит от выбора базиса? Пусть 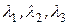 – собственные значения оператора в
– собственные значения оператора в 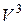 : а) каков его характеристический многочлен; б*) чему равен определитель матрицы оператора?
: а) каков его характеристический многочлен; б*) чему равен определитель матрицы оператора?
6.14. Как находить собственные значения и собственные векторы линейного оператора в n -мерном пространстве?
6.15. Что такое оператор простого типа? Как выглядит матрица оператора в базисе из собственных векторов? Каково достаточное условие оператора простого типа? Является ли оно необходимым?* Что означает диагонализуемость матрицы?
6.16. Матрица оператора в некотором базисе – треугольная. Каковы собственные значения этого оператора?
6.17*. Показать, что оператор, заданный матрицей  (см. вопрос 3.8 из типового расчета №1), переводит базисный вектор
(см. вопрос 3.8 из типового расчета №1), переводит базисный вектор  в
в 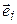 , а остальные базисные векторы – в нуль. Пользуясь этим, вычислить
, а остальные базисные векторы – в нуль. Пользуясь этим, вычислить 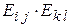 .
.
6.18*. Интерпретируя матрицу А как матрицу линейного оператора, вычислить 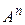 , где: а) А – треугольная матрица n -го порядка с нулевыми элементами на главной диагонали;
, где: а) А – треугольная матрица n -го порядка с нулевыми элементами на главной диагонали;
б) 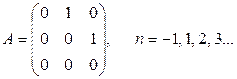 .
.
6.19*. Справедливо ли рассуждение: “Пусть 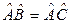 , где
, где  – ненулевой оператор; сократив на
– ненулевой оператор; сократив на 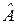 , получим
, получим  ”?
”?
6.20*. Привести пример линейных операторов 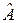 и
и 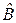 , для которых
, для которых  (указание: см. 6.17*).
(указание: см. 6.17*).
Date: 2015-04-23; view: 1668; Нарушение авторских прав