
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Теорема 9 (Ван-Обеля). Если отрезки АА1, ВВ1, СС1, где А1, В1, С1 – точки на сторонах ВС, АС, АВ треугольника АВС, – чевианы с общей точкой Q, то
|
|

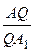 =
= 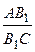 +
+ 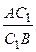 .
.
Доказательство. Проведем прямую l через точку А параллельно ВС. Пусть В 2 и С 2 точки пересечения прямой l с прямыми ВQ и СQ (рис. 98).
Поскольку D В 2 QС 2  D ВQС, то
D ВQС, то 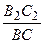 =
= 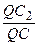 .
.
Из подобия D QАС 2 и D QА 1 С следует 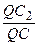 =
= 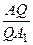 . Поэтому
. Поэтому 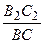 =
= 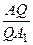 , или
, или 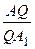 =
= 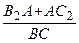 , или
, или 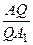 =
= 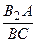 +
+ 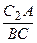 .
.
Поскольку D АС 1 С 2  D ВС 1 С и D АВ 1 В 2
D ВС 1 С и D АВ 1 В 2  D СВ 1 В, то
D СВ 1 В, то 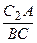 =
= 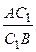 и
и 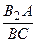 =
= 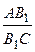 . Тогда
. Тогда 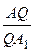 =
= 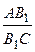 +
+ 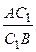 .
.
Следствие 11. Если Q – центр тяжести треугольника АВС и А 1 – середина стороны ВС, то АQ: QА 1 = 2.
Действительно, по теореме Ван-Обеля 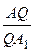 =
= 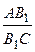 +
+ 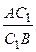 =
=  +
+  = 2.
= 2.
Следствие 12. Если Q – центр вписанного в треугольник АВС круга и А 1 – основание биссектрисы угла А, то АQ: QА 1 =  , а = ВС, b = АС, с = АВ.
, а = ВС, b = АС, с = АВ.
Действительно. С учетом теоремы о биссектрисе угла по теореме Ван-Обеля будем иметь 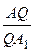 =
= 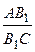 +
+ 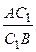 =
= 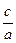 +
+ 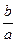 =
=  .
.
Следствие 13. Если Q – точка пересечения Жеогона и А 1 – точка аксания вписанного круга со стороной ВС, то 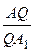 =
= 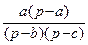 .
.
Учтя теорему 11.3, по теореме Ван-Обеля имеем 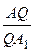 =
= 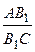 +
+ 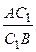 =
=
= 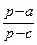 +
+ 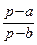 = (р – а)
= (р – а) 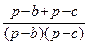 = (р – а)
= (р – а) 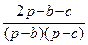 =
= 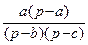 .
.
Следствие 14. Если Q – точка Нагеля и А 1 – точка касания вневписанного круга со стороной ВС, то АQ: QА 1 = а: (р – а).
Сучетом следствия 1 по теореме Ван-Обеля:
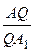 =
= 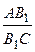 +
+ 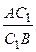 =
= 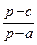 + +
+ + 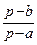 =
= 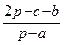 =
= 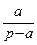 .
.
Теорема 10 (Жаргона). Если Q – точка пересечения чевиан АА 1, ВВ 1, СС 1 треугольника АВС, то 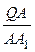 +
+ 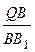 +
+ 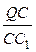 = 1 и
= 1 и 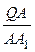 +
+ 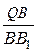 +
+ 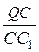 = 2.
= 2.
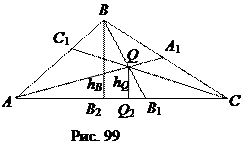 Доказательство. Поскольку D ВВ 2 В 1
Доказательство. Поскольку D ВВ 2 В 1  D QQ 2 В 1 (Ð ВВ 2 В 1 = Ð QQ 2 В 1 = 90°, Ð В 1 – общий), то
D QQ 2 В 1 (Ð ВВ 2 В 1 = Ð QQ 2 В 1 = 90°, Ð В 1 – общий), то
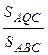 =
= 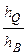 =
= 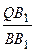 .
.
Аналогично получим, 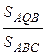 =
= 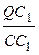 ,
, 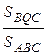 =
= 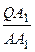 .
.
Тогда 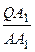 +
+ 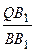 +
+ 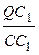 =
= 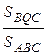 +
+ 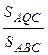 +
+ 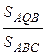 =
= 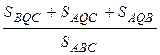 = 1. Первое из необходимых равенств доказано.
= 1. Первое из необходимых равенств доказано.
Поскольку QА = АА 1 – QА 1, то 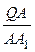 = 1 –
= 1 – 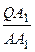 .
.
Аналогично, 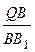 = 1 –
= 1 – 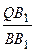 ,
, 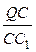 = 1 –
= 1 – 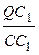 .
.
Поэтому 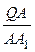 +
+ 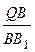 +
+ 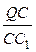 = (1 –
= (1 – 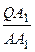 ) + (1 –
) + (1 – 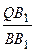 ) + (1 –
) + (1 – 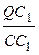 ) =
) =
= 3 – (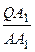 +
+ 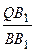 +
+ 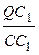 ) = 3 – 1 = 2.
) = 3 – 1 = 2.
Теорема 11 (Карно). Сумма R + r радиусов окружностей, описанной около треугольника и вписанной в него, равна d 1 + d 2 ± d 3, d 1 Ù d 2 Ù d 3, где d 1, d 2, d 3 – расстояния от центра описанной окружности до сторон треугольника, при этом знак минус для тупоугольного треугольника.
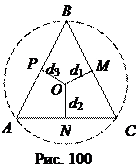 Доказательство. Пусть О – центр описанной около треугольника АВС окружности, М, N, Р – основания перепндикуляров, опущенных из точки О на стороны ВС, АС, АВ соответственно, т.е. МО, NО, РО – серединные перпендикуляры к сторонам треугольника АВС.
Доказательство. Пусть О – центр описанной около треугольника АВС окружности, М, N, Р – основания перепндикуляров, опущенных из точки О на стороны ВС, АС, АВ соответственно, т.е. МО, NО, РО – серединные перпендикуляры к сторонам треугольника АВС.
Пусть треугольник АВС – остроугольный (рис. 100). Тогда рr = SABC = SAOB + SBOC + SAOC = 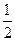 АВ ОР +
АВ ОР + 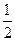 ВС ОМ +
ВС ОМ +
+ 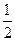 АС ОN =
АС ОN = 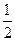 с d 3 +
с d 3 + 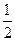 a d 1 +
a d 1 + 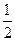 b d 2.
b d 2.
Поскольку четырёхугольник АРОN имеет два противоположных прямых угла, то его можно вписать в окружность. Применив к нему теорему Птолемея, получим
АО РN = ОР АN + ОN АР, или R 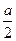 = d 3
= d 3 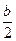 + d 2
+ d 2 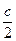 .
.
Аналогично, R 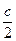 = d 1
= d 1 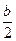 + d 2
+ d 2 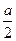 , R
, R 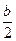 = d 1
= d 1 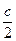 + d 3
+ d 3 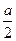 .
.
Сложив три последних равенства, получим
R р = d 1 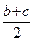 + d 2
+ d 2 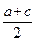 + d 3
+ d 3 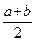 .
.
Поэтому Rр + rp = (d 1 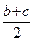 + d 2
+ d 2 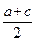 + d 3
+ d 3 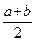 ) +
) + 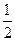 d 1 a +
d 1 a + 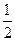 d 2 b +
d 2 b + 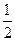 d 3 c =
d 3 c =
= d 1 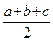 + d 2
+ d 2 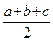 + d 3
+ d 3 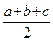 = (d 1 + d 2 + d 3) p.
= (d 1 + d 2 + d 3) p.
Значит, R + r = d 1 + d 2 + d 3.
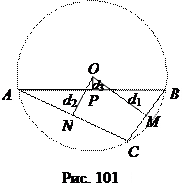 Пусть теперь треугольник АВС – тупоугольный (рис. 101). Тогда
Пусть теперь треугольник АВС – тупоугольный (рис. 101). Тогда
рr = SABC = SСOB + SАOC – SAOВ = 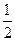 а d 1 +
а d 1 + 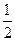 b d 2 –
b d 2 – 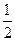 c d 3. Поскольку четырёхугольники ОРМВ, ОМСN, ОРNА – вписанные, то по теореме Птолемея:
c d 3. Поскольку четырёхугольники ОРМВ, ОМСN, ОРNА – вписанные, то по теореме Птолемея: 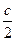 d 1 = d 3
d 1 = d 3 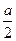 + R
+ R 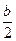 ,
,
R 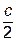 = d 1
= d 1 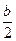 + d 2
+ d 2 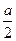 ,
, 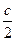 d 2 = d 3 + R
d 2 = d 3 + R  .
.
Из этих равенств получим
R  + R
+ R 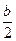 + R
+ R 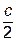 = (
= (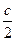 d 1 –
d 1 – 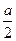 d 3) + (d 1
d 3) + (d 1 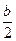 + d 2
+ d 2 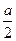 ) + (
) + (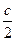 d 2 – d 3
d 2 – d 3 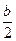 ).
).
Значит, rp + Rр = (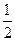 а d 1 +
а d 1 + 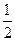 b d 2 –
b d 2 – 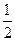 c d 3) + (d 1
c d 3) + (d 1 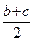 + d 2
+ d 2 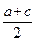 – d 3
– d 3 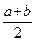 ) =
) =
= d 1 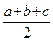 + d 2
+ d 2 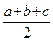 – d 3
– d 3 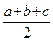 = (d 1 + d 2 – d 3) p.
= (d 1 + d 2 – d 3) p.
Задача 4. Многоугольник, который может быть вписан в круг, разделен непересекающимися диагоналями на треугольники. Доказать, что сумма диаметров кругов, вписанных в эти треугольники, не зависит от того, как проведены диагонали
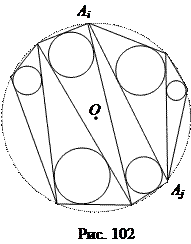 Доказательство. Пусть O – центр круга, описанного около данного многоугольника, А 1 А 2… Аn. Тогда в этот круг будут вписаны все треугольники, возникающие при проведении диагоналей.
Доказательство. Пусть O – центр круга, описанного около данного многоугольника, А 1 А 2… Аn. Тогда в этот круг будут вписаны все треугольники, возникающие при проведении диагоналей.
Для каждого треугольника можно применить теорему Карно
R + rк = d 1 к + d 2 к ± d 3 к .
Правила для выбора знака “+” или ”–“ можно интерпретировать так: знак “+” перед величиной перпендикуляра d 3 к ставится тогда, когда треугольник и центр круга О лежат по одну сторону от прямой, к которой проводится перепендикуляр, и ”–“ – если лежат по разные стороны.
Учитывая, что каждая диагональ разделяет два смежных треугольника, расстояние до этой смежной стороны для одного треугольника будет входить в сумму со знаком “+”, а для дркгого со знаком ”–“. При сложении равенств для R + rк, записанных для всех треугольников, расстояния до диагоналей взаимно сокращаются и в сумме останутся только расстояния di от центра О до сторон многоугольника. Поэтому
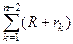 =
= 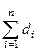 , откуда
, откуда 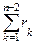 =
= 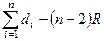 .
.
Последнее равенство показывает, что сумма радиусов, а значит и диаметров, вписанных в треугольники кругов, не зависит от того, как проведены диагонали.
Date: 2015-05-05; view: 5055; Нарушение авторских прав