Углы и окружности

5.1. Иногда приходится рассматривать окружность в пересечении с углом, стороны которого имеют с окружностью общие точки. Вершина угла может совпадать с центром окружности, лежать на самой окружности, быть внутренней точкой круга, лежать вне круга.

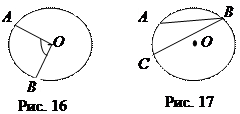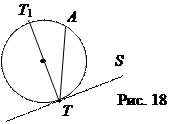
Если вершина угла совпадает с центром, то угол называют центральным, и он измеряется дугой, на которую опирается. На рис. 16 Ð АОВ = АВ. Если вершина угла принадлежит окружности, то его называют вписанным, и он измеряется половиной дуги, на которую опирается. На рис. 17 Ð АВС = АС.

Теорема 1. Угол между касательной и хордой, проведённой через точку касания, измеряется половиной дуги, заключённой между хордой и касательной.

Доказательство. Пусть сторона TS угла ATS является касательной, а сторона ТА – хордой (рис. 18). Проведём диаметр ТТ ₁. Если АТ содержит α , то АТ ₁ содержит

180 – α . Ð АТТ ₁ = (180 – α ) = 90 – α .

Ð АТS = 90 – Ð АТТ ₁ = 90 – ( 90 – α ) = α .

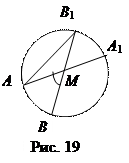5.2. Теорема 2. Угол с вершиной внутри круга измеряется полусуммой дуг, заключённых между сторонами угла и между их продолжениями.

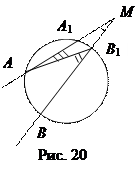
Доказательство. Пусть угол АМВ имеет вершину внутри круга (рис. 19).

Поскольку Ð АМВ – внешний угол для D АВМ ₁,

то Ð АМВ = Ð АВ ₁ М + Ð В ₁ АМ = Ð АВ ₁ В + Ð В ₁ АА ₁ =

= АВ + А ₁ В ₁ = ( АВ + А ₁ В ₁ ).

Теорема 3. Угол с вершиной вне круга измеряется половиной разности дуг, заключённых между его сторонами.

Доказательство. Пусть угол АМВ имеет вершину вне круга (рис. 20). Поскольку углы АМВ ₁ и МАВ ₁ вместе равны внешнему углу АВ ₁ В треугольника АМВ ₁, то

Ð АМВ ₁ = Ð АВ ₁ В – Ð А ₁ АВ ₁ = АВ – А ₁ В ₁ =

= ( АВ – А ₁ В ₁).

Следствие 1. ГМТ, размещённых по одну сторону от прямой, из которых данный отрезок виден под данным углом, есть дуга окружности, которая имеет своими концами концы данного отрезка.

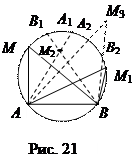Действительно, если из точки М отрезок АВ виден под углом a (рис. 21), то из любой другой точки М ₁ дуги АМВ он виден под этим же углом. Если же взять точку М ₂ между дугой АМВ и отрезком АВ, то Ð АМ ₂ В > Ð АМВ, поскольку Ð АМ ₂ В измеряется полусуммой дуг АВ и А ₁ В ₁, что больше АВ.

Если взять точку М ₃ вне сегмента АМВ, то Ð АМ ₃ В < Ð АМВ, поскольку Ð АМ ₃ В = ( АВ – А ₂ В ₂) < АВ.

Следствие 2. ГМТ, из которых данный отрезок виден под прямым углом, есть окружность, для которой этот отрезок является диаметром.

5.3. Четыре произвольные точки плоскости за редким исключением не попадают на окружность, так как три из них уже определяют окружность, а четвёртая может на ней и не оказаться.

Теорема 4. Если точки А, В, С, D лежат на окружности (в названном порядке) (рис.22), то Ð АВС + Ð ADC = 180 , Ð BAD + Ð BCD = 180 .

Доказательство. Легко получается из теоремы об измерении вписанного угла:

Ð АВС = АDC, Ð ADC = АBC и

Ð АВС + Ð ADC = ( АDC + АBC) = · 360 = 180 .

Второе равенство устанавливается аналогично.

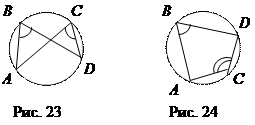
Следствие 3. Если точки А, В, С, D лежат на окружности, то

Ð АВD = Ð ACD (рис. 23) или Ð АВD + Ð ACD = 180 (рис. 24).

Теорема 5. Если точки А, В, С, D плоскости размещены так, что В и С лежат по одну сторону от прямой АD и Ð ABD = Ð ACD или В и С лежат по разные стороны от прямой АD и Ð ABD + Ð ACD = 180 , то точки А, В, С, D принадлежат одной окружности.

Доказательство. Пусть точки В и С лежат по одну сторону от прямой АD и Ð ABD = Ð ACD (рис. 23). Тогда точка С принадлежит ГМТ, для которых отрезок АD виден под углом АВD.

Пусть точки В и С лежат по разные стороны от прямой АD и Ð ABD + Ð ACD = = 180 . Проведём окружность через точки А, В, D. Пусть прямая АС пересекает дугу АD в точке С ₁ (рис. 25). Точка С может находиться между А и С ₁, совпадать с С ₁, лежать на луче АС ₁, вне отрезка АС ₁.

Пусть С ₂ – произвольная точка между А и С ₁. Тогда Ð АС ₂ D – внешний угол треугольника С ₂ С ₁ D и

Ð ABD + Ð AC ₂ D > Ð ABD + Ð AC ₁ D = 180 .Поэтому точка С не может лежать между А и С ₁. Пусть С ₃ – произвольная точка луча АС, находящаяся вне отрезка АС ₁. Тогда Ð AC ₃ D < Ð AC ₁ D (внутренний угол треугольника менше внешнего, не смежного с ним) и Ð ABD + Ð AC ₃ D < Ð ABD + Ð AC ₁ D = 180 . Видим, что точка С не может лежать вне отрезка АС ₁. Поэтому С совпадает с С ₁.

Следствие 4. Для каждого четырёхугольника АВСD (рис. 26) следующие условия эквивалентны:

1. Ð А + Ð С = 180 ; 2. Ð В + Ð D = 180 ;

3. Ð 1 = Ð 4; 4. Ð 2 = Ð 7;

5. Ð 3 = Ð 6; 6. Ð 5 = Ð 8.

Следствие 5. Каждое из условий 1) – 6) (следствие 4) достаточно для того, чтобы около четырёхугольника АВСD можно было описать окружность.

Date: 2015-05-05; view: 916; Нарушение авторских прав