
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Теорема 1. Произведение секущей, проведённой через точку М вне круга, на её внешнюю часть есть величина постоянная
|
|
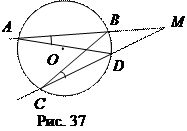 Доказательство. Пусть проведены секущие МА и МС к окружности с центром О из точки М вне круга. Докажем, что МА
Доказательство. Пусть проведены секущие МА и МС к окружности с центром О из точки М вне круга. Докажем, что МА  МВ = МС
МВ = МС  МD.
МD.
 Поскольку Δ АDМ ~ Δ СВМ (Ð А = Ð С – как вписанные углы, опирающиеся на одну и туже дугу ВD, Ð М – общий), то
Поскольку Δ АDМ ~ Δ СВМ (Ð А = Ð С – как вписанные углы, опирающиеся на одну и туже дугу ВD, Ð М – общий), то 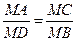 , откуда МА
, откуда МА  МВ = МС
МВ = МС  МD.
МD.
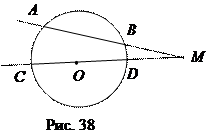
Следствие 1. Произведение секущей, проведённой через точку М, находящуюся на расстоянии а от центра круга
радиуса R, а > R, на её внешнюю часть равна а 2 – R 2.
Действительно, по теореме 1:
МА  МВ = МС
МВ = МС  МD = (а + R) (a – R) = a 2 – R 2 (рис. 38).
МD = (а + R) (a – R) = a 2 – R 2 (рис. 38).
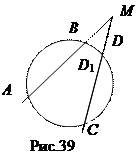 Теорема 2. Если на сторонах угла с вершиной М взяты 4 точки А, В, С, D (рис. 39) такие, что МА
Теорема 2. Если на сторонах угла с вершиной М взяты 4 точки А, В, С, D (рис. 39) такие, что МА  МВ = МС
МВ = МС  МD, то точки А, В, С, D лежат на одной окружности.
МD, то точки А, В, С, D лежат на одной окружности.
Доказательство. Пусть через точки А, В, С проведена окружность и D 1 – её вторая точка пересечения с прямой МС. Тогда по теореме 1: МА  МВ = МС
МВ = МС  МD 1, кроме того по условию МА
МD 1, кроме того по условию МА  МВ = МС
МВ = МС  МD. Тогда МС
МD. Тогда МС  МD 1 = МС
МD 1 = МС  МD. Поэтому точки D 1 и D совпадают.
МD. Поэтому точки D 1 и D совпадают.
 Теорема 3. Если через точку М внутри круга проведена хорда, то произведение частей хорды, на которые она делится точкой М, есть величина постоянная.
Теорема 3. Если через точку М внутри круга проведена хорда, то произведение частей хорды, на которые она делится точкой М, есть величина постоянная.
Доказательство. Пусть через точку М внутри круга с центром О произвольно проведены две хорды АВ и СD. Докажем, что МА  МВ = МС
МВ = МС  МВ (рис. 40). Из подобия Δ АМС и Δ ВМD, (Ð АМС = Ð ВМD, Ð САВ = Ð СDВ) имеем
МВ (рис. 40). Из подобия Δ АМС и Δ ВМD, (Ð АМС = Ð ВМD, Ð САВ = Ð СDВ) имеем 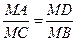 , или МА
, или МА  МВ = МС
МВ = МС  МD.
МD.
Следствие 2. Произведение частей хорды, на которые она делится точкой М, находящейся на расстоянии а от центра круга радиуса R, а < R, равно R 2 – а 2.
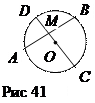 Действительно, по теореме 2 (рис. 41)
Действительно, по теореме 2 (рис. 41)
МА  МВ = МС
МВ = МС  МD = (R + a) (R – a) = R 2 – а 2.
МD = (R + a) (R – a) = R 2 – а 2.
Теорема 4. Если отрезки АВ и СD пересекаются в точке М и МА  МВ = МС
МВ = МС  МD, то точки А, В, С, D принадлежат одной окружности.
МD, то точки А, В, С, D принадлежат одной окружности.
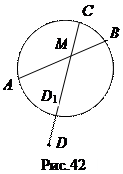 Доказательство. Через точки А, В, С проведём окружность (рис. 42). Пусть D 1 – её вторая точка пересечения с прямой СМ. Тогда по теореме 3 МА
Доказательство. Через точки А, В, С проведём окружность (рис. 42). Пусть D 1 – её вторая точка пересечения с прямой СМ. Тогда по теореме 3 МА  МВ = МС
МВ = МС  МD 1, а по условию МА
МD 1, а по условию МА  МВ = МС
МВ = МС  МD. Тогда МС
МD. Тогда МС  МD 1 = МС
МD 1 = МС  МD, или МD 1 = МD, и, значит точки D 1 и D совпадают.
МD, или МD 1 = МD, и, значит точки D 1 и D совпадают.
Теорема 5. Произведение секущей, проведённой через точку М вне круга, на её внешнюю часть равно квадрату касательной (рис. 43).
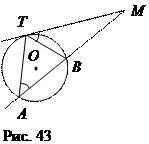 Доказательство. Из подобия Δ АТМ и Δ ВТМ (Ð М – общий, Ð А = Ð ВТМ) имеем
Доказательство. Из подобия Δ АТМ и Δ ВТМ (Ð М – общий, Ð А = Ð ВТМ) имеем 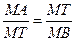 , или МА
, или МА  МВ = МТ 2.
МВ = МТ 2.
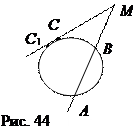 Теорема 6. Если на сторонах угла с вершиной М взяты точки А, В, С (рис. 44) так, что МА
Теорема 6. Если на сторонах угла с вершиной М взяты точки А, В, С (рис. 44) так, что МА  МВ = МС 2, то МС – касательная к окружности, проведённой через точки А, В, С.
МВ = МС 2, то МС – касательная к окружности, проведённой через точки А, В, С.
Доказательство. Проведём окружность через точки А, В, С. Пусть С 1 – вторая точка пересечения прямой МС с этой окружностью. Тогда по теореме 1 МС  МС 1 = МА
МС 1 = МА  МВ. Но по условию МА
МВ. Но по условию МА  МВ = МС 2. Поэтому МС
МВ = МС 2. Поэтому МС  МС 1 = МС 2, или МС 1 = МС. Значит, точки С 1 и С совпадают. Прямая МС имеет с окружностью общую точку и поэтому она – касательная.
МС 1 = МС 2, или МС 1 = МС. Значит, точки С 1 и С совпадают. Прямая МС имеет с окружностью общую точку и поэтому она – касательная.
Задача 1. В круг поместили замкнутую ломанную из пяти звеньев одинаковой длинны. Каждое звено ломаной продолжили до пересечения с окружностью отрезками зелёного и синего цвета, причём из одной вершины ломаной выходят отрезки разного цвета. Доказать, что сумма длин зелёных отрезков совпадает с суммой длин синих.
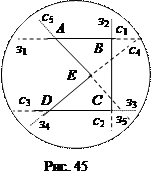 Доказательство. Пусть звенья ломаной АВСDЕ, находящейся в круге, имеют длину а, зі и сі – длины отрезков, продолжающих і-ое звено ломаной до окружности (рис. 45). По теореме 3 будем иметь
Доказательство. Пусть звенья ломаной АВСDЕ, находящейся в круге, имеют длину а, зі и сі – длины отрезков, продолжающих і-ое звено ломаной до окружности (рис. 45). По теореме 3 будем иметь
с 1 (а + з 1 ) = з 5 (а + с 5 ),
с 2 (а + з 2 ) = з 1 (а + с 1 ),
с 3 (а + з 3 ) = з 2 (а + с 2 ),
с 4 (а + з 4 ) = з 3 (а + с 3 ),
с 5 (а + з 5 ) = з 4 (а + с 4 ).
Сложив эти равенства и отбросив равные произведения с 1 з 1, с 2 з 2, с 3 з 3, с 4 з 4, с 5 з 5 из обеих частей, получим (с 1 + с 2 + с 3 + с 4 + с 5 ) а = (з 1 + з 2 + з 3 + + з 4 + з 5 ) а, откуда следует искомое равенство.
7.2. Из теорем 1 и 3 следует, что величина a 2 – R 2 является характеристикой взаимного расположения круга и точки из плоскости круга, где а – расстояние от точки до центра круга, R – радиус круга. Величину a 2 – R 2 называют степенью точки по отношению к кругу.
Теорема 7. ГМТ, которые имеют одну и ту же степень в отношении двух кругов, есть перпендикуляр к линии их центров.
 Доказательство. Пусть О и О 1 – центры кругов с радиусами R и R 1 (рис. 46). Пусть точка М имеет одинаковые степени по отношению к двум кругам. Тогда
Доказательство. Пусть О и О 1 – центры кругов с радиусами R и R 1 (рис. 46). Пусть точка М имеет одинаковые степени по отношению к двум кругам. Тогда
ОМ 2 – R 2 = O 1 M 2 – R 12, откуда
ОМ 2 – O 1 M 2 = R 2 – R 12.
По следствию 4.3 точка М принадлежит определённому перпендикуляру к прямой ОО 1. Пусть N –произвольная точка перпендикуляра к прямой ОО 1, который определён условием ОМ 2 – O 1 M 2 = R 2 – R 12.
Тогда ОN 2 – O 1 N 2 = R 2 – R 12, или ОN 2 – R 2 = O 1 N 2 – R 12.
Последнее равенство означает, что точка N имеет одинаковые степени по отношению к двум кругам. Доказательство остаётся в силе, если, например, R 1 = 0.
Следствие 3. ГМТ, степени которых по отношению к заданной точке равны, есть перпендикуляр к прямой, которая проходит через эту точку и центр окружности.
ГМТ, о которых идёт речь в теореме 7 и следствии 3, называются радикальной осью двух кругов и радикальной осью круга и точки соответственно.
Следствие 4. Два концентрических круга не имеют радикальной оси.
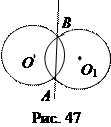 Следствие 5. Радикальная ось двух пересекающихся кругов проходит через точки пересечения соответствующих окружностей.
Следствие 5. Радикальная ось двух пересекающихся кругов проходит через точки пересечения соответствующих окружностей.
Действительно, степени точек А и В (рис. 47) по отношению к каждому из кругов О и О 1 равны нулю.
 Следствие 6. Радикальная ось касающихся кругов совпадает с их общей касательной, проведённой через точку касания.
Следствие 6. Радикальная ось касающихся кругов совпадает с их общей касательной, проведённой через точку касания.
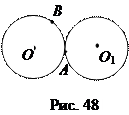
Действительно, если бы радикальная ось имела с окружностью О одну, кроме А, общую точку В (рис. 48), то эта точка должна была иметь степень О и в отношении к кругу О 1. Поэтому она принадлежала бы и окружности О 1. Но окружности не имеют других общих точек, кроме А. Поэтому радикальная ось является касательной к окружности О, и значит, к кругу О 1.
Следствие 7. Радикальные оси любых двух из трёх окружностей или параллельны, или пересекаются в одной точке.
Действительно, если какие-нибудь две из трёх радикальных осей имеют общую точку, то через неё пройдёт и третья радикальная ось.
Date: 2015-05-05; view: 2890; Нарушение авторских прав