Биссектрисы треугольника

Из школы известно, что три биссектрисы внутренних углов треугольника пересекаются в одной точке – центре вписанной в этот треугольник окружности.

Теорема 1. Биссектриса угла А треугольника АВС точкой пересечения биссектрис делится в отношении 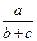, считая от стороны, где а, b, с – длины сторон ВС, АС, АВ соответственно.

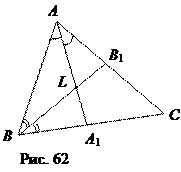Доказательство. Пусть АА ₁ и ВВ ₁ – биссектрисы углов А и В соответственно в треугольнике АВС, L – их точка пересечения, а, b, с – длины сторон ВС, АС, АВ соответственно (рис.62). Тогда по теореме о биссектрисе, применённой к треугольнику АВС будем иметь

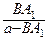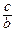= , или b ВА ₁ = ас – с ВА ₁, или ВА ₁ (b + с) = ас, значит, ВА ₁ = 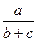с. По этой же теореме, примененной к треугольнику АВА ₁ получим А ₁ L: LА = 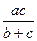: с, или = .

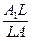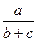Теорема 2. Если L – центр вписанного в треугольник АВС круга, то

Ð АLВ = 90° + Ð С.

Доказательство. Учитывая, что сумма углов треугольника равна 180° и что центр L вписанного круга является точкой пересечения биссектрис треугольника, будем иметь (рис. 62):

Ð АLВ = 180° – (Ð АВL + Ð ВАL) = 180° – (Ð АВС + Ð ВАС) =

= 180° – (180° – Ð С) = 180° – 90° + Ð С = 90° + Ð С.

Теорема 3. Если L – точка на биссектрисе угла С треугольника АВС такая, что Ð АLВ = 90° + Ð С, то L – центр вписанного в треугольник АВС круга.

Доказательство. Докажем, что ни одна из точек L ₁ между C и L не может являтся центром вписанного круга (рис. 62а).

Имеем Ð АL ₁ С ₁ < Ð АLС ₁, так как внешний угол треугольника АL ₁ L больше любого внутреннего угла, не смежного с ним. Так же Ð ВL ₁ С < Ð ВLС ₁.

Поэтому Ð АL ₁ В < Ð АLВ = 90° + Ð С. Значит, L ₁ не является центром вписанного круга, так как не выполнено условие признака центра вписанного круга (см. теорему 2).

Если же точка L ₂ на биссектрисе СС ₁ не принадлежит отрезкуу СL, то Ð АL ₂ В > Ð АLВ = 90° + Ð С и снова не выполнено условие признака центра вписанного круга. Значит, центром вписанного круга является точка L.

Теорема 4. Расстояние от вершины треугольника до точки касания вписанного круга со стороной, проходящей через эту вершину, равно полупериметру этого треугольника, уменьшенному на противоположную сторону.

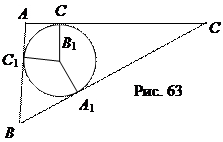Доказательство. Пусть А ₁, В ₁, С ₁ – точки касания вписанного круга со сторонами треугольника АВС (рис. 63), а, b, с – длины сторон ВС, АС, АВ соответственно.

Пусть АС ₁ = х, Тогда АВ ₁ = х, ВС ₁ = с – х = ВА ₁, В ₁ С = b – х = СА ₁,

а = ВС = ВА ₁ + СА ₁ = (с – х) + (b – х) = с + b – 2 х.

Тогда а + а = а + b + с – 2 х, или 2 а = 2 р – 2 х, или х = р – а.

Теорема 5. В любом треугольнике АВС через точку L пересечения биссектрис двух внешних его углов проходит биссектриса третьего угла, при этом точка L находится на одинаковых расстояниях от прямых, содержащих стороны треугольника.

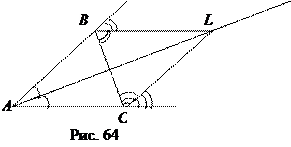Доказательство. Пусть L – точка пересечения двух внешних углов В и С треугольникаа АВС (рис. 64). Поскольку каждая точка биссектрисы находится на одинаковом расстоянии от сторон угла, то точка L находится на одинаковом расстоянии от прямых АВ и ВС, так как она принадлежит биссектрисе ВL. Она же находится на одинаковом расстоянии от прямых ВС и АС, так как принадлежит биссектрисе СL. Поэтому точка L находится на одинаковом расстоянии прямых АВ, АС и ВС. Поскольку точка L находится на одинаковом расстоянии от прямых АВ и АС, то АО – биссектриса угла ВАС.

Окружность, которая касается стороны треугольника и продолжений двух других сторон, называют вневписанной в этот треугольник окружностью.

Следствие 1. Центры вневписанных в треугольник окружностей находятся в точках пересечения пар биссектрис его внешних углов.

Теорема 6. Радиус вписанной в треугольник окружности равен отношению стороны этого трегольника и косинуса половины противолежащего угла, умноженному на синусы половин двух остальных углов:

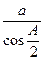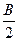r = sin sin .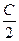

Доказательство. Пусть L – центр вписанной в треугольник АВС окружности, А ₁ – точка её касания со стороной ВС, а – длина стороны ВС (рис. 65). По теореме синусов, применённой к треугольнику ВLС, получим

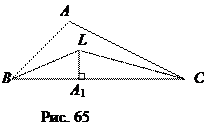
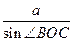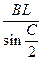= , откуда ВL = =

= = .

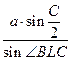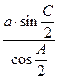Поэтому из прямоугольного треугольника ВLА ₁ имеем

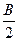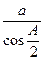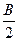r = LA ₁ = BL sin = sin sin .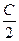

Date: 2015-05-05; view: 1817; Нарушение авторских прав