Теорема синусов

8.1. Теорема синусов позволяет находить стороны треугольника по одной стороне и углах: .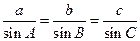

8.2. Теорема 1. В каждом треугольнике отношение любой его стороны и синуса противолежащего угла есть величина постоянная, равная диаметру описанного около этого треугольника круга.

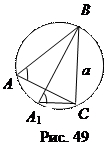Доказательство. Пусть около треугольника АВС описан круг с центром О (рис. 49). Докажем, что .

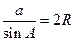Проведём диаметр ВА ₁ и рассмотрим D А ₁ ВС.

В нём Ð А ₁ СВ = 90°, Ð А ₁ = Ð А; ВС = а. ВС = А ₁ В sin A ₁.

Поэтому а = 2 R sin A, или .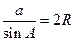

Теоремы синусов и косинусов позволяют найти все элементы треугольника по трём его известным элементам, из которых хотя бы один линейный.

Задача 1. Найти длину биссектрисы угла А треугольника АВС, если его стороны равны а, b, с.

Решение. Пусть в треугольнике АВС: ВС = а, АС = b, АВ = с и АL – биссектриса угла А.

По теореме о биссектрисе (теорема 6.1.)

ВL: LС = АВ: АС.

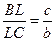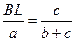Поэтому , или или , или

ВL = .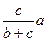

По теореме косинусов, применённой к треугольникам АВС и АВL, будем иметь:

b ² = а ² + с ² – 2 ас соsÐ В и АL ² = ВL ² + с ² + 2 с ВL соsÐ В.

Тогда

АL ² = 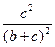а ² + с ² – 2 с 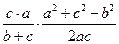= с ² ( 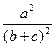+ 1 – ) =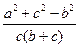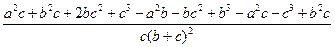

=с ² = с ² =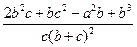

= bс 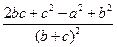= 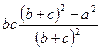и АL = l_a = = .

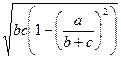Задача 2. Найти радиус окружности, проходящей через одну из вершин квадрата со стороной а, его центр и середину стороны, не содержащую указанную вершину.

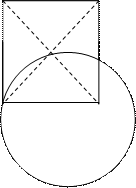B C Решение. Пусть О – центр квадрата АВСD со стороной а,

М – середина стороны СD. Нужно вычислить радиус

окружности, которой принадлежат точки А, О и М (рис. 52).

О М По теореме 1: , .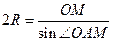

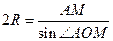А D Поскольку ОМ = а, ОА = 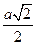, АМ = 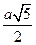, Ð АОМ = 135°, то

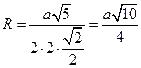
Рис. 51

Date: 2015-05-05; view: 852; Нарушение авторских прав