Медианы треугольника

Теорема 1. Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2: 1, считая от вершины.

Доказательство. Пусть АА ₁ и ВВ ₁ – медианы треугольника АВС, М – точка их пересечения (рис. 52). Поскольку А ₁ В ₁ – средняя линия треугольника АВС, то А ₁ В ₁ ||АВ и А ₁ В ₁ = АВ.

Тогда Ð МА ₁ В ₁ = Ð МАВ, Ð МВ ₁ А = Ð МВ ₁ А ₁ – как 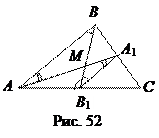внутренние накрестлежащие при параллельных прямых АВ и А ₁ В ₁ и секущей АА ₁ (для первого равенства) и секущей ВВ ₁ (для другого равенства).

Поэтому D МАВ D МА ₁ В ₁. и = 2: 1.

Пусть медианы АА ₁ и СС ₁ пересекаются в точке N. Тогда АN: NA ₁ = 2: 1, значит, точки М и N совпадают.

Точку пересечения медиан треугольника называют ещё центром тяжести треугольника.

Это название можно объяснить следующим образом. Пусть АВС – треугольная однородная пластина. Если представить её разделённой на очень узкие пластины, как показано на рисунке 53, то легко понять, что центры тяжести этих пластин находятся на медиане АА ₁. Поэтому центр тяжести пластины находится в определённой точке медианы АА ₁. Так же устанавливается, что центр тяжести пластины АВС находится и на медиане ВВ ₁, а значит, в точке пересечения медиан АА ₁ и ВВ ₁.

Иной раз бывает полезным при решении задач, связанных с медианой треугольника, продолжить её на такое же расстояние за точку пересечения со стороной треугольника.

Задача 1. Найти площадь треугольника со сторонами 6 и 8, если медиана, проведённая к третьей стороне, равна 5.

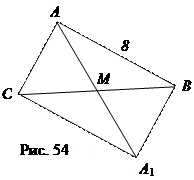Решение. Пусть в D АВС: АВ = 8, АС = 6 и медиана АМ = 5. Продолжим медиану АМ за точку М на расстояние 5, получим точку А ₁. Поскольку АВА ₁ С – параллелограмм, то треугольники АВС и АА ₁ С имеют равные площади.

В треугольнике АА ₁ С все три стороны известны:

АС = 6, А ₁ С = 8, АА ₁ = 2 АМ = 10.

Поэтому .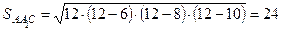

§ 10. Высоты треугольника

Теорема 1. Три прямые, содержащие высоты треугольника, пересекаются в одной точке.

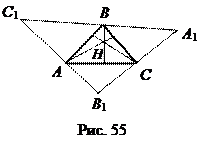
Доказательство. Через вершины треугольника АВС проведены прямые, параллельные противоположным сторонам. Тогда получим D А ₁ В ₁ С ₁ (рис. 55).

Поскольку АС ₁ ВС и АВА ₁ С – параллелограммы, то АС = С ₁ В = ВА ₁. Значит В – середина стороны А ₁ С ₁. Так же: А – середина стороны В ₁ С ₁, С – середина стороны А ₁ В ₁. Высоты треугольника АВС являются серединными перпендикулярами к сторонам треугольника А ₁ В ₁ С ₁, поскольку АВ||А ₁ В ₁, ВС||В ₁ С ₁, АС||А ₁ С ₁.

Поскольку серединные перпендикуляры D А ₁ В ₁ С ₁ пересекаются в одной точке, то совпадающие с ними прямые, содержащие высоты D АВС, пересекаются в одной точке. Точку Н пересечения высот D АВС называют его ортоцентром.

Теорема 2. Для каждого треугольника его ортоцентр Н, центр О описанной окружности и центр тяжести М лежат на одной прямой, причём ОМ: МН = 1: 2.

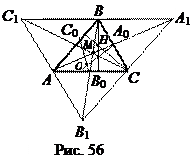Доказательство. Пусть Н – ортоцентр треугольника АВС, М – точка пересечения его медиан, О – точка пересечения перпендикуляров к сторонам.

Через вершины А, В, С проведём прямые, параллельные сторонам треугольника АВС. В полученном треугольнике А ₁ В ₁ С ₁ стороны треугольника АВС являются средними линиями (рис. 56). Поскольку АВА ₁ С – параллелограмм, то прямая АМ пройдёт через А ₁ и А ₀ – середину стороны ВС. Так же прямая ВМ пройдёт через В ₁, а СМ – через С ₁. Поэтому D АВС и D А ₁ В ₁ С ₁ имеют общий центр тяжести – точку М.

Рассмотрим гомотетию 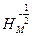.При этом преобразовании: А ₁ ® А, В ₁ ® В, С ₁ ® С. Поэтому D А ₁ В ₁ С ₁ перейдёт в D АВС, поскольку отрезок переходит в отрезок. Центр описанного около треугольника А ₁ В ₁ С ₁ круга перейдёт в центр О описанного около треугольника АВС круга. Но центром описанного около треугольника А ₁ В ₁ С ₁ круга является, как установлено в доказательстве теоремы 1, ортоцентр Н треугольника АВС. Значит, точки Н и М лежат на прямой, проходящей через центр М гомотетии. Кроме того, НМ: МО = 2: 1 (с учетом коэффициента гомотетии).

Прямую, которой принадлежит ортоцентр треугольника, его центр тяжести и центр описанного круга, называют прямой Эйлера.

Теорема 3. Для любого треугольника АВС середины его сторон и основания высот лежат на одной окружности, которая делит пополам отрезки от вершин треугольника до ортоцентра. Центр этой окружности лежит на прямой Эйлера и делит пополам отрезок между ортоцентром Н и центром О описанного круга.

Середины отрезков от вершин до ортоцентра называют точками Эйлера.

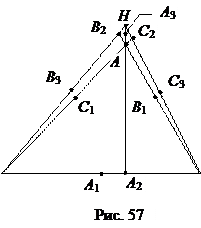
Доказательство. Пусть А ₁, В ₁, С ₁ – середины сторон треугольника АВС (рис. 57), А ₂, В ₂, С ₂ – основания его высот, А ₃, В ₃, С ₃ – середины отрезков АН, ВН, СН, где Н – ортоцентр. Будем иметь: А ₁ В ₁ ||АВ и А ₁ В ₁ = АВ, поскольку А ₁ В ₁ – средняя линия треугольника АВС; А ₃ В ₃ ||АВ и А ₃ В ₃ = АВ, поскольку А ₃ В ₃ – средняя линия D АВН;

А ₁ В ₃ ||НС и А ₁ В ₃ = НС, как средняя линия треугольника ВСН; А ₃ В ₁ ||НС и

А ₃ В ₁ = НС, как средняя линия треугольника НСА. Отсюда следует, что А ₁ В ₁ А ₃ В ₃ – параллелограмм. Поскольку СН ^ АВ, А ₃ В ₁ ||НС, А ₃ В ₃ ||АВ, то А ₃ В ₁ ^ А ₃ В ₃, и поэтому А ₁ В ₁ А ₃ В ₃ – прямоугольник.

Так же доказывается, что А ₁ С ₁ А ₃ С ₃ – прямоугольник.

Поскольку отрезки А1А3, В1В3 и С1С3 являются диагоналями этих прямоугольников, то они пересекаются в одной точке Q. Поэтому точки А1, В1, С1, А3, В3, С3 лежат на одной окружности с центром Q.

Точка А ₂ находится на этой окружности, поскольку Ð А ₁ А ₂ А ₃ = 90°. Так же устанавливаем, что В ₂ находится на окружности с диаметром В ₁ В ₃, а С ₂ – на окружности с диаметром С ₁ С ₃, т.е. на одной и той же окружности. Центр Q этой окружности находится на серединном перпендикуляре к хорде А ₁ А ₂, который делит пополам отрезок ОН, где О – центр описанной около треугольника АВС окружности. Действительно, А ₁ О ^ ВС, А ₂ Н ^ ВС, поэтому перпендикуляр к А ₁ А ₂ делит пополам отрезок ОН, будучи параллельным А ₁ О и А ₂ Н. Так же серединный перпендикуляр к хорде В ₁ В ₂ содержит центр Q окружности и проходит через середину отрезка ОН. Значит, Q – середина ОН.

Окружность, которая проходит через середины сторон треугольника, основания его высот и делит пополам отрезки от вершин до ортоцентра, называется окружностью девяти точек, или окружностью Эйлера.

Следствие 1. Диаметр окружности Эйлера равен радиусу описанной около треугольника окружности.

Действительно, окружность Эйлера можно рассматривать, как окружность, описанную около треугольника А ₁ В ₁ С ₁ из средних линий (рис. 58). Поскольку треугольник АВС подобен треугольнику А ₁ В ₁ С ₁ с коэффициентом подобия 2, то радиус описанной около треугольника АВС окружности вдвое больше радиуса окружности, описанной около треугольника А ₁ В ₁ С ₁, значит он равен диаметру окружности девяти точек.

Теорема 4 (Гамильтона). Если Н – ортоцентр треугольника АВС, то треугольники АВС, АВН, ВСН, АСН имеют общую окружность девяти точек.

Доказательство. Пусть в треугольнике АВС: Н – ортоцентр, А ₁, В ₁, С ₁– середины сторон, А ₂, В ₂, С ₂ – основания высот, А ₃, В ₃, С ₃ – точки Эйлера (середины отрезков, 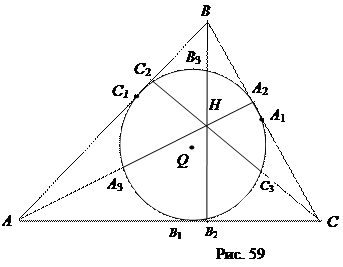соединяющих ортоцентр с вершинами) (Рис.59). По теореме 3 все эти точки принадлежат окружности Эйлера треугольника АВС. Три из этих точек А ₃, С ₁, С ₂ – принадлежат окружности Эйлера треугольника АВН: А ₃ – середина стороны АН, С₁ – середина стороны АВ, С ₂ – основание перпендикуляра НС ₂. Поскольку окружность однозначно определяется тремя точками, то окружность Эйлера треугольника АВН совпадает с окружностью Эйлера треугольника АВС.

Следствие 2. Радиусы окружностей, описанных около треугольников АВС, АВН, ВСН, АСН, равны.

Действительно, каждый из названных радиусов равен диаметру окружности Эйлера (следствие 1), а поэтому они равны между собой.

Теорема 5 (Файербаха). Окружность девяти точек касается вписанной окружности и трёх вневписанных окружностей.

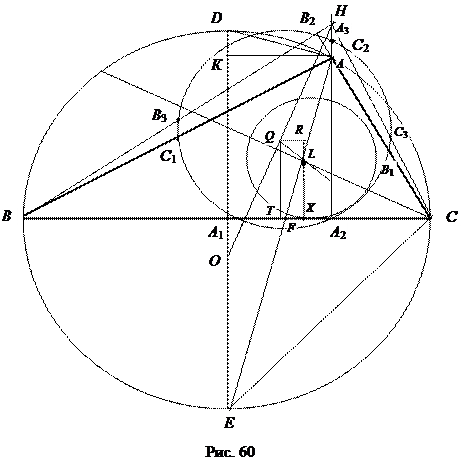Доказательство. Пусть, А ₁, В ₁, С ₁ – середины сторон треугольника АВС, А ₂, В ₂, С ₂ – основания его высот, А ₃, В ₃, С ₃ – точки Эйлера, L – точка пересечения биссектрис AF и CN треугольника АВС, Q – центр окружности Эйлера треугольника АВС, О – центр круга, описанного около треугольника АВС, Н – ортоцентр треугольника АВС (рис.60).

Чтобы доказать касание вписанной окружности и окружности Эйлера, достаточно доказать, что расстояние между их центрами L и Q равна разности радиуса R_Q окружности Эйлера и r_L вписанной окружности.

Из точки Q опустим перпендикуляр ОR на LХ, LХ ^ АВ. Из треугольника QRL найдем QL ² = QR ² + RL ². Поскольку QR = А ₁ Х – А ₁ Т и RL = QТ – LХ, то

QL ² = (А ₁ Х – А ₁ Т)² + (QТ – LХ)².

Докажем, что QТ = ОК, где К – основание перпендикуляра АК на DЕ, DЕ – серединный перпендикуляр к ВС. Через точку Е проходит биссектриса АЕ угла ВАС.

Точки А ₁, А ₃ принадлежат окружности Эйлера, А ₁ А ₃ – диаметр этой окружности, ОА – радиус описанной окружности. По следствию 1: А ₁ А ₃ = ОА. Поскольку ОА ₁ ||АА ₃, то А ₁ А ₃ АО – параллелограмм. Значит, ОА ₁ = АА ₃, и ОК = А ₂ А ₃. Поскольку А ₂ и А ₃ принадлежат окружности Эйлера, то QА ₂ А ₃ – равнобедренный треугольник. Значит, QТ = А ₂ А ₃, или QТ = ОК. Поскольку QТ – перпендикуляр к хорде А ₁ А ₂, то А ₁ Т = А ₁ А ₂.

Поэтому QL ² = (А ₁ Х – А ₁ А ₂)² + + ( ОК – LХ)² =

= А ₁ Х ² + 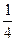А ₁ А ₂² – А ₁ Х А ₁ А ₂ + 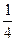ОК ² + LХ ² – ОК LХ =

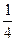= А ₁ А ₂² + 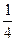ОК ² + LХ ² – ОК LХ + А ₁ Х ² – А ₁ Х А ₁ А ₂ =

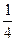= (А ₁ А ₂² + ОК ²) + LХ ² – ОК LХ + А ₁ Х (А ₁ Х – А ₁ А ₂) =

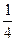= ( ОА ² + LХ ²) – ОК LХ – А ₁ Х (А ₁ А ₂ – А ₁ Х) = ( 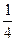ОА ² + LХ ²) – ОК LХ – А ₁ Х ХА ₂ =

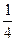= ( ОА ² + LХ ²) – (ОК LХ + А ₁ Х ХА ₂) = ( + r ²) – (ОК LХ + А ₁ Х ХА ₂).

Теперь докажем, что А ₁ Х ХА ₂ = KD LX.

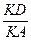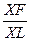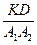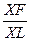Имеем D АКD D LXF, где F – точка пересечения АЕ с ВС, поскольку они имеют взаимно перпендикулярные стороны. Поэтому = , или = , или

KD LX = А ₁ А ₂ ХF (1).

Остается доказать, что А ₁ А ₂ ХF = А ₁ Х ХА ₂.

Имеем D EFC D EAC: LE – общая; Ð ECF = Ð EAC, как углы, которые опираются на равные дуги ВЕ и СЕ. Поэтому = .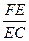

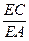Треугольник LEС – равнобедренный: Ð LCЕ = 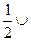NBE;

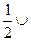Ð ELC = ( ЕС + АN) = ( ЕВ + NВ) = NBE.

Поэтому 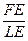= 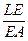. Это 4 отрезка прямой ЕА. Заменим эти отрезки их проекциями на ВС: 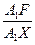= 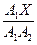, или А ₁ F А ₁ А ₂ = А ₁ Х ².

Вычитая компоненты этого равенства от А ₁ А ₂ А ₁ Х, получим:

А ₁ А ₂ А ₁ Х – А ₁ F А ₁ А ₂ = А ₁ А ₂ А ₁ Х – А ₁ Х ² или

А ₁ А ₂ (А ₁ Х – А ₁ F) =А ₁ Х (А ₁ А ₂ – А ₁ Х) или

А ₁ А ₂ (А ₁ Х – А ₁ F) = А ₁ Х ХА ₂ или А ₁ А ₂ ХF = А ₁ Х ХА ₂.

Тогда

KD LX = А ₁ Х ХА ₂ = А ₁ А ₂ ХF.

Теперь равенство (1) можно записать так KD LX = А ₁ Х ХА ₂.

Поэтому QL ² = ( + r ²) – (ОК LХ + KD LX) = ( + r ²) – LХ (ОК + KD) =

= ( + r ²) – LХ ОD = ( + r ² – r R = 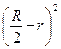= 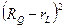. Это значит, что окружность Эйлера касается вписанной окружности.

Теорема 6. Произведение двух сторон треугольника равно произведению диаметра описанного круга на высоту, проведенную к третьей стороне.

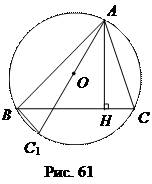Доказательство. Пусть в треугольнике АВС: АН – высота, проведенная к стороне ВС, АС ₁ – диаметр описанного около этого треугольника круга (рис. 61).

Поскольку LC = LС ₁, то прямоугольные треугольники АНС и АВС ₁ подобны. Поэтому 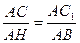, и АВ АС = А С₁ АН.

Следствие 3. Радиус описанного около треугольника круга равен произведению двух его сторон, поделенному на удвоенную высоту, проведенную к третьей стороне: R = .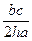

Date: 2015-05-05; view: 1518; Нарушение авторских прав