
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Теорема Фалеса
|
|
Теорема Фалеса является основанием для теории подобия фигур.
Теорема Фалеса: Если две прямые а и а 1 пересечены рядом параллельных прямых и на прямой а при этом отсекаются равные отрезки, то и на прямой а 1 отсекаются так же равные отрезки (рис. 27).
Доказательство. Пусть на прямой а параллельные прямые АА 1, ВВ 1, СС 1, DD 1 отсекают равные отрезки АВ и CD. Докажем, что отрезки А 1 В 1 и С 1 D 1 отсечённые этими прямыми на прямой а 1, так же равны.
Проведём ВМ || а 1, DN || a 1 и рассмотрим 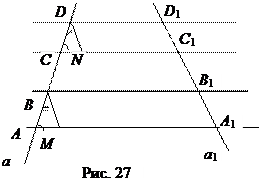
треугольники АВМ и СDN.
У них: 1) АВ = СD по условию;
2) Ð ВАМ = Ð DCM, как соответствующие
углы при пересечении параллельных прямых АА 1и СС 1 секущей АС;
3) Ð АВМ = Ð CDN, как соответствующие углы при пересечении параллельных прямых
ВМ и DN секущей BD.
Значит, Δ АВМ = Δ CDN и поэтому DN = ВМ. А поскольку DD 1 C 1 N и BB 1 A 1 M – параллелограммы, то С 1 D 1 = DN, А 1 В 1 = ВМ и, значит, А 1 В 1 = С 1 D 1.
Теорему Фалеса можно легко обобщить на тот случай, если отрезки АВ и СD на прямой а соизмеримы, например, если АВ: СD = m: n, m, n 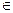 N.
N.
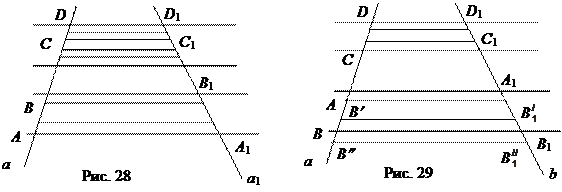
На рисунке 28 показаны дополнительные построения для доказательства того, что если АВ: СD = 3: 5, то А 1 В 1: С 1 D 1 = 3: 5.
 |
Если отрезки АВ и СD не соизмеримы, то для каждого натурального n существуют такие точки B¢ и B², что В принадлежит отрезку B¢B² и
АВ¢: СD = mn: n, АВ²: СD = (mn + 1): n.
Тогда А 1 B 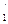 : СD = mn: n и А 1 B
: СD = mn: n и А 1 B 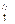 : С 1 D 1 = (mn + 1): n и В Î [B
: С 1 D 1 = (mn + 1): n и В Î [B 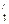 B
B 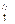 ]. Поэтому если последовательность
]. Поэтому если последовательность 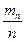 сходится к иррациональному числу, то АВ: СD = a: 1 и А 1 В 1: С 1 D 1 = a: 1 (рис. 29).
сходится к иррациональному числу, то АВ: СD = a: 1 и А 1 В 1: С 1 D 1 = a: 1 (рис. 29).
 |
Следствие 1. Прямая PQ, параллельная одной из сторон треугольника, делит две другие стороны на пропорциональные части (рис. 30).
Следствие 2. Если прямая делит две стороны треугольника на пропорциональные части, то она параллельна третьей стороне.
Действительно, если провести PQ 1 ║ ВС (рис.30), то АВ: АВ = АQ 1: АС, а по условию АР: АВ = АQ: АС, значит АQ = АQ 1 и Q = Q 1.
Теорема 1 (о биссектрисе). В каждом треугольнике биссектриса любого угла делит противолежащую сторону на части пропорционально прилегающим сторонам.
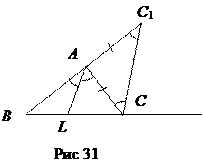 Доказательство. Пусть AL – биссектриса угла А треугольника АВС. Докажем, что ВL: LС = АВ: АС. Проведём СС 1 ║ АL (рис. 31). Тогда ВL: LС = ВА: АС 1. Ð ВАL = Ð ВС 1 С как соответствующие углы при параллельных прямых AL и СС 1 и секущей ВС 1; Ð АСС 1 = Ð САL как внутренние накрест лежащие при параллельных прямых AL и СС 1 и секущей АС.
Доказательство. Пусть AL – биссектриса угла А треугольника АВС. Докажем, что ВL: LС = АВ: АС. Проведём СС 1 ║ АL (рис. 31). Тогда ВL: LС = ВА: АС 1. Ð ВАL = Ð ВС 1 С как соответствующие углы при параллельных прямых AL и СС 1 и секущей ВС 1; Ð АСС 1 = Ð САL как внутренние накрест лежащие при параллельных прямых AL и СС 1 и секущей АС.
Значит, Δ АСС 1 – равнобедренный: АС = АС 1.
Поэтому ВL: LС = ВА: АС = АВ: АС.
Следствие 3. Если прамая, выходящая из вершины треугольника, пересекает противолежащую сторону и делит её на части, пропорциональные прилежащим сторонам, то она является биссектрисой угла треугольника.
Теорема 2. В каждом треугольнике биссектриса внешнего угла делит противолежащую сторону внешним образом на части, пропорциональные прилежащим сторонам.
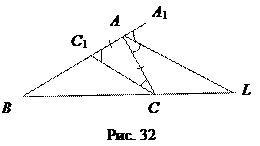 Доказательство. Пусть АL – биссектриса внешнего угла А треугольника АВС. Докажем, что ВL: СL = АВ: АС.
Доказательство. Пусть АL – биссектриса внешнего угла А треугольника АВС. Докажем, что ВL: СL = АВ: АС.
Проведем СС 1║ АL. Тогда ВL: СL = ВА: С 1 А. Кроме того, Δ АСС 1 – равнобедренный: Ð АСС 1 = Ð САL как внутренние накрест лежащие при параллельных прямых AL и СС 1 и секущей АС; Ð АС 1 С = Ð А 1 АL, как соответствующие углы при параллельных прямых АL и С 1 С и секущей АС 1. Поэтому АС 1 = АС и
ВL: СL = АВ: АС.
Следствие 4. Если прямая, выходящая из вершины треугольника, пересекает продолжение противоположной стороны и делит её на части, пропорциональные прилежащим сторонам, то эта прямая содержит биссектрису внешнего угла треугольника.
Доказательство. Поскольку есть только одна точка, которая делит внешним образом сторону ВС на части, пропорциональные прилежащим сторонам, то эта точка совпадает с основанием биссектрисы внешнего угла треугольника.
 Теорема 3. Геометрическое место точек, расстояния которых до двух данных точек находятся между собой в данном отношении, отличным от 1, есть окружность.
Теорема 3. Геометрическое место точек, расстояния которых до двух данных точек находятся между собой в данном отношении, отличным от 1, есть окружность.
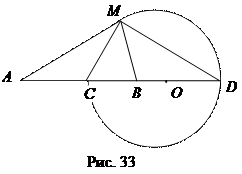
Доказательство. Пусть А и В – данные точки. Нужно найти ГМТ М таких, что АМ: МВ = k, k ¹ 1 (рис. 33). Есть одна точка С, которая делит отрезок АВ в отношении k внутренним образом и одна точка D, которая делит этот отрезок в этом отношении внешним образом. Пусть М – произвольная точка искомого ГМТ. Тогда
АМ: МВ = k = АС: СВ и АМ: МВ = АD: ВD.
Поэтому МС и МD – биссектрисы внутреннего и внешнего углов М треугольника АМВ. Поскольку биссектрисы смежных углов перпендикулярны, то Ð СМD = 90° и точка М принадлежит окружности с диаметром СD.
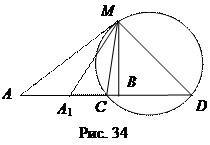 Пусть теперь М – произвольная точка окружности с диаметром CD. Проведём МА 1 так, что Ð СМВ = Ð СМА 1 (рис. 34). Тогда МС – биссектриса угла А 1 МВ треугольника А 1 МВ. МD – биссектриса внешнего угла с вершиной М этого треугольникатак как Ð СМD = 90°.
Пусть теперь М – произвольная точка окружности с диаметром CD. Проведём МА 1 так, что Ð СМВ = Ð СМА 1 (рис. 34). Тогда МС – биссектриса угла А 1 МВ треугольника А 1 МВ. МD – биссектриса внешнего угла с вершиной М этого треугольникатак как Ð СМD = 90°.
По теоремам 1, 2
А  М: МВ = А
М: МВ = А  С: СВ и А
С: СВ и А  М: МВ = А
М: МВ = А  D: ВD.
D: ВD.
Поэтому А  С: СВ = А
С: СВ = А  D: ВD, или ВD: СВ = А
D: ВD, или ВD: СВ = А  D: А
D: А  С. А поскольку
С. А поскольку
АС: СВ = k и АD: DВ = k, то АС: СВ = АD: DВ, или ВD: СВ = АD: АС.
Значит, А  D: А
D: А  С = АD: АС. Это равенство означает, что точки А и А
С = АD: АС. Это равенство означает, что точки А и А  делят отрезок СD в одном и том же отношении, причем внешним образом. Значит, точка А
делят отрезок СD в одном и том же отношении, причем внешним образом. Значит, точка А  совпадает с точкой А. Поэтому АМ: МВ = АС: СD = k, т.е. точка М принадлежит искомому ГМТ.
совпадает с точкой А. Поэтому АМ: МВ = АС: СD = k, т.е. точка М принадлежит искомому ГМТ.
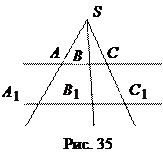 Теорема 4. Прямые, проходящие через одну точку и пересекающие параллельные прямые, отсекают на них пропорциональные отрезки.
Теорема 4. Прямые, проходящие через одну точку и пересекающие параллельные прямые, отсекают на них пропорциональные отрезки.
Доказательство. Пусть АС || А  С
С  и прямые АА
и прямые АА  , ВВ
, ВВ  , СС
, СС  проходят через точку S (рис. 35).
проходят через точку S (рис. 35).
Докажем, что АВ: А  В
В  = ВС: В
= ВС: В  С
С  .
.
Из подобия Δ АSB  Δ A
Δ A  SB
SB  имеем
имеем 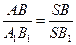 . Из подобия Δ ВSС
. Из подобия Δ ВSС  Δ В
Δ В  SС
SС  имеем
имеем  . Значит,
. Значит, 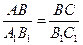 .
.
Теорема 5. Если прямые АА  , ВВ
, ВВ  , СС
, СС  при пересечении с параллельными прямыми АВ и А
при пересечении с параллельными прямыми АВ и А  В
В  образуют пропорциональные отрезки
образуют пропорциональные отрезки
(АВ: А  В
В  = АС: А
= АС: А  С
С  = ВС: В
= ВС: В  С
С  ), то прямые АА
), то прямые АА  , ВВ
, ВВ  , СС
, СС  или параллельны, или проходят через одну точку.
или параллельны, или проходят через одну точку.
Доказательство. Из трёх прямых или никакие две не пересекаются (и тогда они параллельны), или какие-нибудь пересекаются, и третья прямая так же проходит через их точку пересечения.
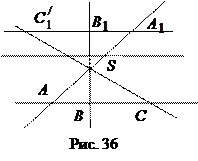 Пусть прямые АА
Пусть прямые АА  и ВВ
и ВВ  пересекаются в точке S (рис. 36). Проведем прямую СS. Пусть С
пересекаются в точке S (рис. 36). Проведем прямую СS. Пусть С 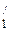 – точка пересечения прямой СS с прямой А
– точка пересечения прямой СS с прямой А  В
В  . Тогда по теореме 4: А
. Тогда по теореме 4: А  С
С 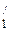 : С
: С 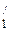 В
В  = АС: СВ. Но по условию:
= АС: СВ. Но по условию:
СВ = А  С
С  : С
: С  В
В  . Поэтому
. Поэтому
А  С
С 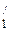 = С
= С 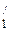 В
В  = А
= А  С
С  : С
: С  В
В  . Поскольку точки С
. Поскольку точки С  и С
и С 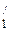 делят отрезок А
делят отрезок А  В
В  в одном и том же отношении или внешним, или внутренним образом, то точки С
в одном и том же отношении или внешним, или внутренним образом, то точки С  и С
и С 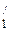 совпадают и прямая SС совпадает с прямой СС
совпадают и прямая SС совпадает с прямой СС  .
.
Date: 2015-05-05; view: 1238; Нарушение авторских прав