
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Площадь
|
|
Площадь – одна из характеристик геометрической фигуры. Она выражается через параметры, определяющие эту фигуру. Очевидно, что формула, по которой определяется площадь фигуры, зависит от вида фигуры и от параметров, её определяющих. Например, для площади треугольника наиболее используемыми являются формулы формулы
S =  ah, S =
ah, S =  ab sin C, S =
ab sin C, S = 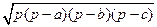 , S = pr, S = 2 R 2 sin A sin B sin C.
, S = pr, S = 2 R 2 sin A sin B sin C.
Задача 1. В равнобедренном треугольнике основание равно 40, высота, проведённая к ней – 15. Найти высоту, проведённую к боковой стороне.
 Решение. Поскольку высота ВD в равнобедренном треугольнике АВС, проведённая к основанию АС, является медианой, то АD =
Решение. Поскольку высота ВD в равнобедренном треугольнике АВС, проведённая к основанию АС, является медианой, то АD =  АС = 20.
АС = 20.
Поэтому АВ = 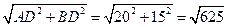 = 25.
= 25.
Площадь треугольника АВС можно выразить формулами
S =  bhb и S =
bhb и S =  chc, откуда bhc = chc, и
chc, откуда bhc = chc, и
hc =  = 24.
= 24.
В задаче 1 нужный параметр фигуры был найденчерез промежуточное использование площади. Этот приём, который называют методом площадей, был использован Пифагором (§ 4).
Задача 2. Найти длину биссектрисы угла треугольника, если визвесты этот угол и стороны, его образующие.
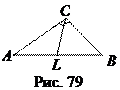 Решение. пусть CL – биссектриса угла С треугольника АВС (рис. 79), СА = b, СВ = а, СL = lс. Поскольку СL разбивает треугольник АВС на два треугольника АСL и ВСL, то с учётом адитивности площади будем иметь:
Решение. пусть CL – биссектриса угла С треугольника АВС (рис. 79), СА = b, СВ = а, СL = lс. Поскольку СL разбивает треугольник АВС на два треугольника АСL и ВСL, то с учётом адитивности площади будем иметь:
SАВС = SАВС + SАВС, или  ab sin C =
ab sin C =  blc sin
blc sin 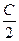 +
+  alc sin
alc sin 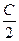 , или 2 ab sin
, или 2 ab sin 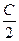 cos
cos 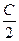 = lc (a + b) sin
= lc (a + b) sin 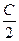 , или lc =
, или lc = 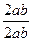 cos
cos 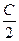 .
.
Теорема 1. Для любого описанного около окружности многоугольника справедливо равенство S = pr, дзе S – площадь многоугольника, р – его полупериметр, r – радиус вписанного круга.
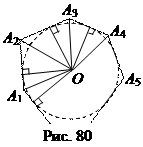 Доказательство. Если многоугольник А 1 А 2 А 3 … А n описан около окружности с центром О, то отрезки ОА 1, ОА 2, … ОА n делят его на n треугольников А 1 ОА 2, А 2 ОА 3, …, А n OA 1, основаниями которых являются стороны многоугольника, а высотами – радиусы, проведённые в точки касания. Поэтому
Доказательство. Если многоугольник А 1 А 2 А 3 … А n описан около окружности с центром О, то отрезки ОА 1, ОА 2, … ОА n делят его на n треугольников А 1 ОА 2, А 2 ОА 3, …, А n OA 1, основаниями которых являются стороны многоугольника, а высотами – радиусы, проведённые в точки касания. Поэтому
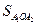 +
+ 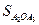 + … +
+ … + 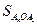 =
=  А 1 А 2 r +
А 1 А 2 r +  А 2 А 3 r + …+
А 2 А 3 r + …+  А n А 1 r =
А n А 1 r =
=  (А 1 А 2 + А 2 А 3 + + … А n А 1) r = p r.
(А 1 А 2 + А 2 А 3 + + … А n А 1) r = p r.
Теорема 2. Для любого треугольника его площад равна произведению радиусаыуса окружности на полупериметр, уменьшенному на сотору, которой касается эта окружность: S = ra (p – a).
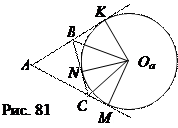 Доказательство. Пусть окружность Оа является вневписанной в треугольник АВС (рис. 81) ОаК, ОаМ, ОаN – радиусы, проведенные в точки касания.
Доказательство. Пусть окружность Оа является вневписанной в треугольник АВС (рис. 81) ОаК, ОаМ, ОаN – радиусы, проведенные в точки касания.
Тогда
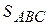 =
= 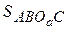 –
–  =
= 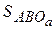 +
+ 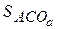 –
–  =
=
=  АВ ra +
АВ ra +  АВ ra –
АВ ra –  АВra =
АВra =  ra (AB + AC – BC) =
ra (AB + AC – BC) =
=  ra (AB + AC + BC – 2 BC) = ra (
ra (AB + AC + BC – 2 BC) = ra (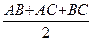 – BC) = ra (p – a).
– BC) = ra (p – a).
Следствие 1. Отрезок касательной от вершины треугольника до противолежащего вневписанного круга равен полупериметру треугольника.
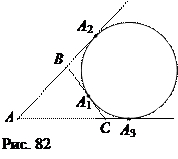 Доказательство. Пусть А 1, А 2, А 3 – точки касания вневписанной окружности со стороной ВС треугольника АВС и продолжений двух других его сторон (рис. 82). Тогда
Доказательство. Пусть А 1, А 2, А 3 – точки касания вневписанной окружности со стороной ВС треугольника АВС и продолжений двух других его сторон (рис. 82). Тогда
АА 2 = АВ + ВА 2 = АВ + ВА 1 = с + ВА 1, АА 3 = АС + СА 3 = = АС + СА 1 = b + СА 1. Поскольку АА 2 = АА 3, то
2 АА 2 = b + c + BA 1 + CA 1 = b + c + BC = a + b + c, откуда АА 2 = 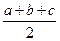 = р.
= р.
Следствие 2. Радиусы вневписанных и вписанной окружности в треугольник связаны равенством 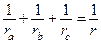 .
.
Действительно, по теореме 2: 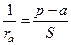 ,
, 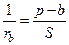 ,
, 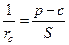 .
.
Тогда 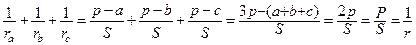 .
.
Следствие 2. 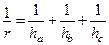 .
.
Действительно, 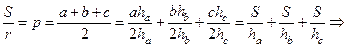
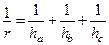 .
.
Теорема 3. ГМТ М, для которых площади треугольников МАВ и МАС равны, где А, В, С – данные точки, есть объединение двух прямых, из которых одна проходит через А параллельно ВС, а другая содержит медиану АК треугольника АВС.
 Доказательство. Пусть точка М 1 принадлежит прямой М 1, проходящей через А параллельно ВС (рис. 83). Тогда
Доказательство. Пусть точка М 1 принадлежит прямой М 1, проходящей через А параллельно ВС (рис. 83). Тогда 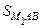 =
=  М 1 А hb =
М 1 А hb = 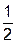 М 1 А hc =
М 1 А hc = 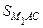 .
.
Пусть точка М 2 принадлежит медиане АК треугольника АВС. Тогда SABK =  ВК hа =
ВК hа =  СК hа = SACK,
СК hа = SACK, 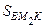 =
=  ВК
ВК 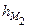 = =
= = 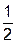 СК
СК 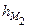 =
= 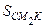 . Значит,
. Значит, 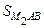 = SABK –
= SABK – 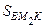 = SACK –
= SACK – 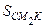 =
= 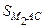 .
.
Аналогично сравниваются площади треугольников МАВ и МАС, если точка М расположена на луче АК за точкой А и на луче АК за точкой К.
Пусть теперь точка N не принадлежит ни одной из названных прямых l и АК. Тогда точка N может находиться:
1) в полосе между прямыми l и ВС, включая прямую ВС;
2) ниже прямой ВС (точки N и В) лежат по разные стороны от ВС;
3) выше прямой l (точки N и В) лежат по разные стороны от прямой l.
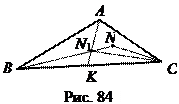 Пусть точка N лежит в полосе между l и ВС внутри треугольника АВС (рис. 84). Тогда один из отрезков СN или ВN, пусть ВN, пересекает медиану АК в точке N 1.
Пусть точка N лежит в полосе между l и ВС внутри треугольника АВС (рис. 84). Тогда один из отрезков СN или ВN, пусть ВN, пересекает медиану АК в точке N 1.
Поскольку 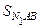 =
= 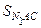 и D N 1 АВ – часть D NАВ, D NАС – часть D N 1 АС, то SNAB >
и D N 1 АВ – часть D NАВ, D NАС – часть D N 1 АС, то SNAB > 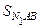 =
= 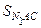 > SNAC.
> SNAC.
Значит, ни одна из внутренних точек треугольника АВС, кроме точек медианы АК не принадлежит искомому ГМТ.
 Пусть теперь точка N так же находится в полосе между l и АС, но вне треугольника АВС (рис. 85). Тогда или отрезок NС пересекает АВ, или отрезок NВ пересекает АС. Пусть NС пересекает АВ в точке Р.
Пусть теперь точка N так же находится в полосе между l и АС, но вне треугольника АВС (рис. 85). Тогда или отрезок NС пересекает АВ, или отрезок NВ пересекает АС. Пусть NС пересекает АВ в точке Р.
Если в сравниваемых треугольниках NАВ и NАС общую часть – треугольник NАР заменить на треугольник РВС, то соотношения между площадьми исходных треугольников NАВ и NАС и полученных треугольников NВС и АВС будут одинаковыми.
Поскольку SNВС.= 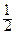 ВС hN <
ВС hN < 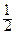 ВС hA = SАВС, то SNAB < SNAC. Значит, точка N не принадлежит искомому ГМТ.
ВС hA = SАВС, то SNAB < SNAC. Значит, точка N не принадлежит искомому ГМТ.
Пусть точка N опять находится в полосе между l и АВ, N ¹ К, и точка N принадлежит ВС, или одному из отрезков АВ или АС. Тогда очевидно, что SNAB ¹ SNAC.
Пусть точка N лежит ниже прямой ВС, причем отрезок АN пересекает отрезок ВС в точке R (рис. 86). Поскольку RВ > RС, то 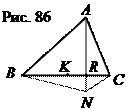 SABR =
SABR = 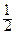 ВR hA >
ВR hA > 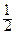 CR hA = SАСR,
CR hA = SАСR,
SNBR.= 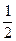 ВRhN >
ВRhN > 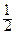 CR hN = SNСR.
CR hN = SNСR.
Значит, SNAB = SABR.+ SNBR.> SАСR + SNСR = SNAC.
Если точка R совпадает с В или S, то, очевидно, что SNAB = SNAC. Значит, такая точка N не принадлежит искомому ГМТ.
Пусть N лежит ниже прямой ВС и отрезок АN не пересекает отрезок ВС. Пусть точка пересечения отрезка АN с прямой ВС принадлежит лучу ВС (рис. 87). В этом случае треугольник NАС является частью треугольника NАВ, поэтому SNAB > SNAC. Значит, такие точки N искомому ГМТ не принадлежат.
 Пусть теперь точка N лежит выше прямой l, причем NС пересекает АВ или NВ. Пусть NС пересекает АВ в точке Q (рис. 88). В этом случае, как и для рис. 85, получим
Пусть теперь точка N лежит выше прямой l, причем NС пересекает АВ или NВ. Пусть NС пересекает АВ в точке Q (рис. 88). В этом случае, как и для рис. 85, получим
SNAB – SNAC = SNQB – SAQC = SNBC – SABC =
= 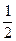 ВC hN –
ВC hN – 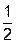 ВC hA =
ВC hA = 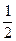 ВC (hN – hA) > 0.
ВC (hN – hA) > 0.
Поэтому все такие точки искомому ГМТ не принадлежат.
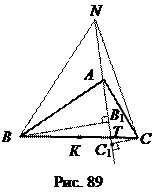 Пусть точка N лежит выше прямой l и отрезки NВ и АС, а так же NС и АВ не имеют общих точек (рис. 89). Пусть прямая NА пересекает ВС в точке Т, отличной от К. Тогда ВТ > СТ. Имеем SNAB =
Пусть точка N лежит выше прямой l и отрезки NВ и АС, а так же NС и АВ не имеют общих точек (рис. 89). Пусть прямая NА пересекает ВС в точке Т, отличной от К. Тогда ВТ > СТ. Имеем SNAB =  NA hB >
NA hB >  NA hC = SNAC, поскольку в подобных прямоугольных треугольниках ВВ 1 Т и СС 1 Т ВТ > СТ, а значит, ВВ 1 = hB > hC = СС 1. Поэтому все такие точки искомому ГМТ не принадлежат.
NA hC = SNAC, поскольку в подобных прямоугольных треугольниках ВВ 1 Т и СС 1 Т ВТ > СТ, а значит, ВВ 1 = hB > hC = СС 1. Поэтому все такие точки искомому ГМТ не принадлежат.
Таким образом, для каждой точки М, принадлежащей прямой l или прямой ВК, площади треугольников МАВ и МАС равны, а если точка N не принадлежит этим прямым, то площади треугольников NАВ т NАС разные.
Теорема 4. Для каждого треугольника радиус R описанной около него окружности и радиусы r вписанной и rа, rb, rc вневписанных окружностей связаны павенством 4 R = rа + rb + rc – r.
Доказательство. С учётом теорем 1 и 2 получим
 =
= 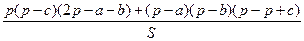 =
= 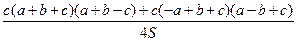 =
=
= 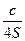 (((a + b)2 – c)2) + (c 2 – (a – b)2) =
(((a + b)2 – c)2) + (c 2 – (a – b)2) = 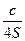 4 ab = 4
4 ab = 4 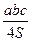 = 4 R.
= 4 R.
Теорема 5. Произведение радиусов вписанной и вневписанных окружностей в треугольник равно квадрату его площади.
Имеем r rа rb rc = 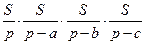 =
= 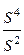 = S 2.
= S 2.
Теорема 6. Площадь четырёхугольника равна половине произведения его диагоналей на синус угла между ними: S =  d 1 d 2 sin j.
d 1 d 2 sin j.
 Доказательство. Пусть d 1 и d 2 – диагонали четырёхугольника АВСD и j – угол между нимиі (рис. 90). Тогда
Доказательство. Пусть d 1 и d 2 – диагонали четырёхугольника АВСD и j – угол между нимиі (рис. 90). Тогда
SABCD = SABC + SADC = 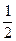 AC hB +
AC hB + 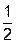 AC hD =
AC hD =
= 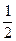 AC (hB + hD) =
AC (hB + hD) = 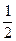 AC (BQ sin j + DQ sin j) =
AC (BQ sin j + DQ sin j) =
= 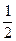 AC (BQ + DQ) sin j = =
AC (BQ + DQ) sin j = = 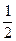 AB BD sin j.
AB BD sin j.
Теорема 7. Если в двух треугольниках по две стороны размещены на пересекающихся прямых, то их площади относятся как произведения этих сторон треугольников.
 Доказательство. Пусть по две стороны в треугольниках АМN и АРQ лежат на прямых АМ и АN, например, как на рис. 91.
Доказательство. Пусть по две стороны в треугольниках АМN и АРQ лежат на прямых АМ и АN, например, как на рис. 91.
Тогда  , поскольку
, поскольку
sin PAQ = sin (180° – MAN) = sin MAN.
Доказательство остаётся в силе и при других возможных размещениях треугольников.
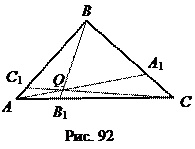 Теорема 8 (Чевы). Для того, чтобы прямые АА 1, ВВ 1, СС 1, где А 1, В 1, С 1 – точки соответственно на сторонах ВС, АС, АВ треугольника АВС, пересекались в одной точке необходимо и достаточно, чтобы
Теорема 8 (Чевы). Для того, чтобы прямые АА 1, ВВ 1, СС 1, где А 1, В 1, С 1 – точки соответственно на сторонах ВС, АС, АВ треугольника АВС, пересекались в одной точке необходимо и достаточно, чтобы 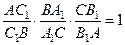 .
.
Доказательство. Пусть отрезки АА 1, ВВ 1, СС 1 пересекаются в точке Q (рис. 92). Тогда треугольник АВС делится на 6 треугольных частей. Поскольку к треугольным частям, прилегающим к одной стороне треугольника АВС, можно применить теорему 6, то
 ;
; 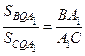 ;
; 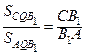 .
.
Поэтому 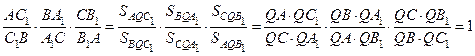 .
.
Последний переход от отношений площадей к отношению произведений сделан на основании теоремы 6.
Пусть теперь точки А 1, В 1, С 1 выбраны на сторонах ВС, АС, АВ треугольника АВС так, что выполняется равенство 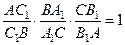 .
.
Пусть Q – точка пересечения отрезков АА 1 и ВВ 1, и С2 – точка пересечения луча СQ с отрезком АВ (рис. 93).
 Тогда, по доказанному ранее
Тогда, по доказанному ранее 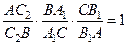 . С учётом условия получим:
. С учётом условия получим: 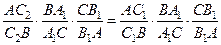 , откуда
, откуда 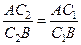 .
.
Полученное равенство показывает, что точки С 1 иі С 2 делят отрезок АВ в одном и том же отношении. Поэтому они совпадают и СС 1 проходит через точку Q.
Следствие 2. Медианы треугольника пересекаются в одной точке.
Следствие 3. Биссектрисы треугольника пересекаются в одной точке.
По теореме о биссектрисе имеем 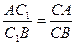 ;
; 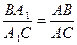 ;
; 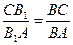 .
.
Тогда 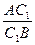
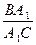
 =
= 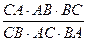 = 1.
= 1.
По теореме Чевы биссектрисы АА 1, ВВ 1, СС 1 пересекаются в одной точке.
Следствие 4. Высоты треугольника пересекаются в одной точке.
Имеем
АС 1 = АС cos A, C 1 B = BC cos B, BA 1 = AB cos B,
A 1 C = AC cos C, CB 1 = BC cos C, B 1 A = AB cos A.
Поэтому 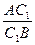
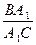
 =
= 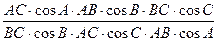 = 1.
= 1.
Следствие 5. Отрезки, соединяющие вершины треугольника с точками касания вписанного в него круга, пересекаются в одной точке, которая называется точкой Жергона.
 Поскольку касательные к кругу, проведенные из одной точки, равны, то (рис.94)
Поскольку касательные к кругу, проведенные из одной точки, равны, то (рис.94)
АС 1 = B 1 A, C 1 B = BA 1, A 1 C = CB 1.
Поэтому 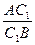
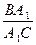
 =
= 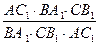 = 1.
= 1.
Следствие 6. Отрезки, соединяющие вершины треугольника с точками касания вневписанных в него окружностей, пересекаются в одной точке, которая называется точкой Нагеля.
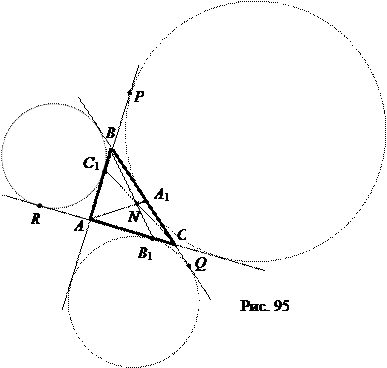 |
Имеем ВА 1 = ВР = АР – АВ = р – с (рис. 95), поскольку АР = р (следствие 13.1). Аналогично, А 1 С = р – b, СВ 1 = р – а, В 1 А = р – с, АС 1 = р – b, С 1 В = р – а. Поэтому
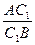
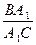
 =
= 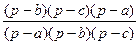 = 1.
= 1.
Прямые, проходящие через вершины треугольника и пересекающиеся в одной точке, называются прямыми Чевы или чевианами.
Следствие 7. Чевианы, проходящие через точку Нагеля, делят периметр треугольника пополам.
Действительно,
АВ + ВА 1 = с + (р – с) = р, ВС + СВ 1 = а + (р – а) = р, СА + АС 1 = b + (р – b) = р.
Следствие 8. Прямые, выходящие из вершин треугольника и делящие противолежащие стороны пропорционально прилежащим углам, являются чевианами.
 Имеем
Имеем 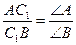 ;
; 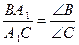 ;
; 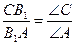 .
.
Поэтому 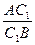
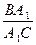
 =
= 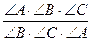 = 1.
= 1.
Следствие 9. Отрезки, соединяющие середины сторон треугольника с серединами прямых Чевы, проведённых из противолежащих вершин, являются чевианами.
 Пусть АА 1, ВВ 1, СС 1 – чевианы треугольника АВС, А 2, В 2, С 2 – середины сторон ВС, АС, АВ, А 3, В 3, С 3 – середины чевиан АА 1, ВВ 1, СС 1. А 2 А 3 – отрезок, соединяющий середину стороны ВС и середину чевианы из вершины А, В 2 В 3 – отрезок, соединяющий середину стороны АС середину чевианы из вершины В, С 2 С 3 – отрезок, соединяющий середину стороны АВ середину чевианы из вершины С (рис.97).
Пусть АА 1, ВВ 1, СС 1 – чевианы треугольника АВС, А 2, В 2, С 2 – середины сторон ВС, АС, АВ, А 3, В 3, С 3 – середины чевиан АА 1, ВВ 1, СС 1. А 2 А 3 – отрезок, соединяющий середину стороны ВС и середину чевианы из вершины А, В 2 В 3 – отрезок, соединяющий середину стороны АС середину чевианы из вершины В, С 2 С 3 – отрезок, соединяющий середину стороны АВ середину чевианы из вершины С (рис.97).
По теореме Чевы получим 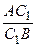
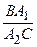
 = 1, откуда
= 1, откуда 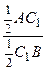
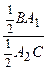
 = 1, или
= 1, или 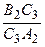
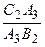
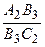 = 1.
= 1.
Отрезки В 2 В 3, С 2 С 3, А 2 А 3, выходящие из вершин треугольника А 2 В 2 С 2, из-за последнего равенства удовлетворяют теореме Чевы, и поэтому пересекаются в одной точке.
Следствие 10 (Теорема Шлёмильха). Отрезки, соединяющие середины сторон треугольника с серединами его высот, являются чевианами.
Легко заметить, что справедливым является утверждение, обратное следствию 9:
Если в треугольнике А 2 В 2 С 2, образованном средними линиями треугольника АВС, проведены чевианы А 2 А 3, В 2 В 3, С 2 С 3, то прямые АА 3, ВВ 3, СС 3, являются чевианами треугольника АВС.
Задача 3. Доказать, что площадь любого треугольника выражается формулой
S = 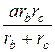 ,
,
где а – сторона треугольника, rb и rc – радиусы вневписанных окружностей, которые касаются сторон b и c соответственно.
Решение. Поскольку rb = 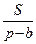 , rс =
, rс = 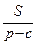 , то
, то 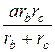 =
= 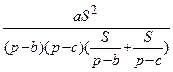 =
=
=  =
= 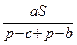 =
= 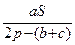 =
=  = S.
= S.
Date: 2015-05-05; view: 1720; Нарушение авторских прав