
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Четырёхугольник
|
|
В школьном курсе геометрии изучаются только отдельные виды четырёхугольников.
Теорема 1 (Вариньона). Середины сторон произвольного четырехугольника являются вершинами параллелограмма, стороны которого параллельны диагоналям четырёхугольника и равны их половинам.
Доказательство. 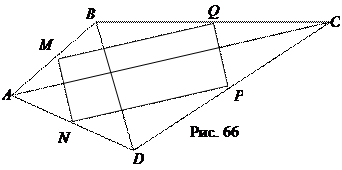 Пусть M, N, P, Q – середины сторон четырёхугольника АВСD (рис. 66). Поскольку MN и PQ – средние линии треугольников АВD и СВD, то MN || BD || PQ, MN =
Пусть M, N, P, Q – середины сторон четырёхугольника АВСD (рис. 66). Поскольку MN и PQ – средние линии треугольников АВD и СВD, то MN || BD || PQ, MN =  BD = PQ.
BD = PQ.
Аналогично получим, что
NP || АС || MQ, NP =  АС = MQ.
АС = MQ.
Теорема 2. Около четырёхугольника, образованного биссектрисами углов данного выпуклого четырёхугольника, можно описать окружность.
 Доказательство. Пусть биссектрисы AQ, DQ, BS и CS
Доказательство. Пусть биссектрисы AQ, DQ, BS и CS
четырёхугольника АВСD образуют четырёхугольник
PQRS (рис. 67).
Докажем, что Ð Q + Ð S = 180°. Действительно,
Ð Q + Ð S = 180° – (Ð QAD + Ð QDA) + 180° –
– (Ð SBC + Ð SCB) = 360° –  (Ð BAD + Ð CDA +
(Ð BAD + Ð CDA +
+Ð ABC + Ð DCB) = 360° –  360° = 180°.
360° = 180°.
Теорема 3 (Бретшнайдера). Квадрат произведения диагоналей четырехугольника равен сумме квадратов произведений его противолежащих сторон без удвоенного произведения всех его сторон на косинус суммы двух противолежащих углов.
 Доказательство. Пусть a, b, c, d – длины сторон четырёхугольника АВСD (рис. 68), m и n – его диагонали. Построим точки М и К так, чтобы
Доказательство. Пусть a, b, c, d – длины сторон четырёхугольника АВСD (рис. 68), m и n – его диагонали. Построим точки М и К так, чтобы
Ð ADМ = Ð BAС, Ð DАМ = Ð BСА, а Ð КАВ = Ð AСD, Ð КВА = Ð САD и Ð КАМ = Ð BAD + Ð BСD.
Тогда D АDМ  D САВ, D АКВ
D САВ, D АКВ  D СDA.
D СDA.
Значит, 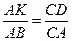 ,
, 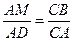 ,
, 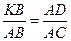 ,
, 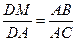 .
.
Тогда АК = 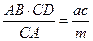 , АМ =
, АМ = 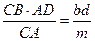 ;
;
КВ = 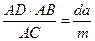 = DМ.
= DМ.
Поскольку Ð КBD + Ð BDМ = (Ð КВА + Ð АBD) +
+ (Ð BDА + Ð ADМ) = (Ð АBD + Ð BDА) + (Ð КВА+
+ Ð ADМ) = (Ð АBD + Ð BDА) +(Ð DАС + Ð САВ) =
= Ð АBD + Ð BDА + Ð BAD = 180°, то ВК || DМ и четырехугольник ВDМК параллелограмм.
Поэтому КМ = ВD = n. По теореме косинусовприменённой к треугольнику АКМ, получим
КМ 2 = АК 2 + АМ 2 – 2 Ак АМ cos Ð KAM, или
 n 2 =
n 2 = 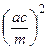 +
+ 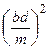 – 2
– 2 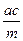 +
+ 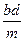 cos (Ð A + Ð C), или
cos (Ð A + Ð C), или
m 2 n 2 = a 2 c 2 + b 2 d 2 – 2 abcd cos (Ð A + Ð C).
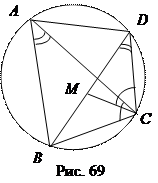
Теорема 4 (Птолемея). Произведение диагоналей вписанного в круг четырёхугольника равно сумме произведений противоположных сторон.
Доказательство. Пусть четырёхугольник АВ С D вписан в окружность (рис. 69). На диагонали ВD возьмем точку М так, что Ð МСD = Ð ВСА. Тогда, учитывая, что Ð ВАС = Ð ВDС, получим D АВС  D DМС. Поэтому
D DМС. Поэтому 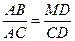 .
.
Из подобия D САD  D СВМ (Ð DАС = Ð МВС,
D СВМ (Ð DАС = Ð МВС,
Ð АСD = Ð DСМ – Ð АСМ = Ð АСВ – Ð АСМ = Ð МСВ) получим  .
.
Из полученных пропорций находим
АВ СD = АС МD и ВС АD = АС МВ, откуда
АВ СD + ВС АD = АС (МD + ВМ) = АС ВD.
Отметим, что теорему Птолемея можно получить в качестве непосредственного следствия из теоремы Бретшнайдера. Действительно, для вписанного в круг четырёхугольника Ð А + Ð С = 180°, поэтому
m 2 n 2 = a 2 c 2 + b 2 d 2 – 2 abcd (–1) = (ас + вd)2.
Теорема 5. Если произведение диагоналей четырёхугольника равно сумме произведений его противолежащих сторон, то около этого четырёхугольника можно описать окружность.
Доказательство. Пусть a, b, c, d – длины последовательных сторон четырёхугольника, m и n – длины его диагоналей, А и С противолежащие углы. Пусть так же mn = aс + bd. Тогда m 2 n 2 = a 2 c 2 + b 2 d 2 + 2 abcd.
По теореме Бретшнайдера имеем
m 2 n 2 = a 2 c 2 + b 2 d 2 – 2 abcd cos (Ð A + Ð C).
Сравнив равенства, получим cos (Ð A + Ð C) = –1, откуда Ð A + Ð C = 180º.
Следствие 1. В любом четырёхугольнике произведение его диагоналей не превышает суммы произведений его противолежащих сторон и больше разности этих произведений.
Действительно, по теореме Бретшнайдера
m 2 n 2 = a 2 c 2 + b 2 d 2 – 2 abcd cos (Ð A + Ð C).
Поскольку –1 < cos (Ð A + Ð C) < 1, то
a 2 c 2 + b 2 d 2 – 2 abcd < m 2 n 2 < a 2 c 2 + b 2 d 2 + 2 abcd,
или | aс – bd | < mn < aс + bd.
Следствие 2. Утверждение теоремы Птолемея остаётся в силе, если пункты А, В, С, D лежат на одной прямой (рис. 70) и АВ = а, ВС = b, СD = с.
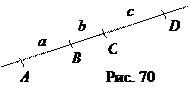 Докажем, что АС ВD = АВ СD + АD ВС.
Докажем, что АС ВD = АВ СD + АD ВС.
Имеем АС ВD = (а + b) (b + c) = ab + b 2 + ac + bc =
= ac + b (a + b + c) = АВ СD = ВС AD.
Отметим, что если прямую рассматривать как окружность бесконечно большого радиуса, то следствие 2 можно рассматривать как частный случай теоремы Птолемея.
Задача 1 (Теорема Помпея). Доказать, что отрезки, соединяющие произвольную точку М плоскости с вершинами правильного треугольника, могут служить сторонами треугольника АВС, если точка М не принадлежит описанной около треугольника АВС окружности. Найти угол треугольника, образованного отрезками АМ, ВМ и СМ, противолежащий стороне ВМ, если Ð АМС = a.
 Решение. По теореме Бретшнайдера, применённой к четырёхугольнику АМСВ, получим
Решение. По теореме Бретшнайдера, применённой к четырёхугольнику АМСВ, получим
АС 2 ВМ 2 = АВ 2 МС 2 + ВС 2 АМ 2 –
– 2 АВ ВС СМ МА cos (60º + Ð АМС).
Учтя, что АВ = ВС = СА, будем иметь
ВМ 2 = МС 2 + АМ 2 – 2 СМ МА cos (60º + Ð АМС).(1)
Поскольку точка М не принадлежит описанной около треугольника АВС окружности, то Ð АМС = 120º. Кроме того, 60º + Ð АМС > 0º. Поэтому
–1 < cos (60º + Ð АМС) < 1 и МС 2 + АМ 2 – 2 СМ МА < ВМ 2 < МС 2 + АМ 2 + 2 СМ МА,
или (MC – MA)2 < ВМ 2 < (MC + MA)2, или | MC – MA | < ВМ < | MC + MA |
Отсюда следует, что существует треугольник со сторонами МА, МВ, МС. Из равенства (1) получим, что угол, противолежащий стороне ВМ, равен 60º +a.
Теорема 6. Диагонали вписанного в круг четырёхугольника относятся как суммы произведений сторон, выходящих из концов этих диагоналей.
Доказательство. Пусть четырёхугольник АВСD вписан в круг, АВ = а,
ВС = b, СD = с, DА = а, АС = m, ВD = n (рис. 72).
Образуем ещё два четырёхугольника с такими же сторонами, вписанные в круг такого же радиуса (рис. 73, 74).
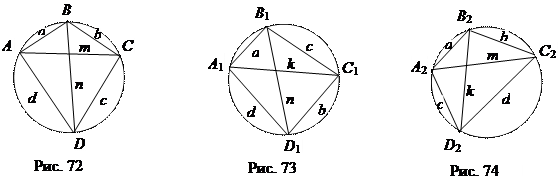 |
Отметим, что существует только три различных вписанных четырёхугольника с данными сторонами a, b, c, d. Действительно, если зафиксировать одну из сторон, например а, то разные четырёхугольники будут отличаться стороной, противолежащей стороне а, а таких возможностей 3 – b, c, d.
Очевидно, что дуга А 2 В 2 С 2 на рис.74 стягивается той же хордой m, что и дуга АВС на рис. 72, дуга В 1 С 1 D 1 – той же хордой n на рис. 73, что и дуга ВСD на рис. 72. Кроме того, дуга А 1 В 1 С 1 на рис. 73 стягивается той же хордой k, что и дуга А 2 В 2 С 2 на рис. 74. Применив к вписанным четырёхугольникам А 1 В 1 С 1 D 1 и А 2 В 2 С 2 D 2 теорему Птолемея, получим равенства nk = ab + cd, mk = bc + ad, откуда 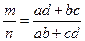 .
.
Отметим, что приведённое доказательство существенно отличается от доказательств, рассмотренных ранее, в которых использовалась фигура, описываемая условием теоремы, возможно с дополнительными построениями. В рассмотренном доказательстве образованы новые фигуры, которые только частично содержат элементы исходной фигуры.
Задача 2. (Последовательные) стороны вписанного в круг четырёхугольника равны a, b, c, d. Найти диагонали четырёхугольника.
Решение. Заметим, что условием задачи – длинами сторон и вписанностью – четырёхугольник определен с точностью следования сторон. Возможны только три случая: (a, b, c, d) (рис. 72), (a, c, b, d) (рис. 73), (a, b, d, c) (рис. 74).
Для случая (a, b, c, d) диагонали четырёхугольника связаны равенствами:
xy = aс + bd (по теореме Птолемея), 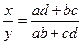 (по теореме).
(по теореме).
Перемножив эти равенства, получим х 2 = 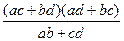 , а поделив первое равенство на второе, получим у 2 =
, а поделив первое равенство на второе, получим у 2 = 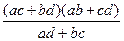 , откуда
, откуда
х 1 = 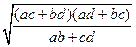 ; у 1 =
; у 1 = 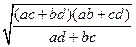 .
.
Для случая (a, c, b, d) аналогично получим:
х 2 =  ; у 2 =
; у 2 = 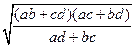 .
.
Наконец, для случая (a, b, d, c) будем иметь:
х 3 = 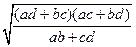 ; у 3 =
; у 3 = 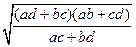 .
.
Теорема 7. Если четырёхугольник АВСD описан около круга, то суммы противолежащих его сторон равны: АВ + СD = АD + ВС.
 Доказательство. Пусть M, N, P, Q – точки касания круга со сторонами четырёхугольника АВСD (рис. 75).
Доказательство. Пусть M, N, P, Q – точки касания круга со сторонами четырёхугольника АВСD (рис. 75).
Поскольку касательные к кругу, проведённые из одной точки, равны, то АМ = АQ, BM = BN, CP = CN, DP = DQ. Сложив почленно эти равенства получим
АМ + ВМ + СР + DР = АQ + ВN + СN + DQ, или
АВ + СD = АD + ВС.
Теорема 8. Если суммы противоположных сторон четырёхугольника равны, то в него можно вписать круг.
 Доказательство. Пусть четырёхугольник АВСD такой, что
Доказательство. Пусть четырёхугольник АВСD такой, что
АВ + СD = АD + ВС. (1)
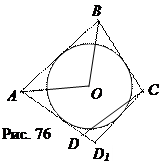
Проведём биссектрисы углов А и В. Тогда точка их пересечения находится на одинаковом расстоянии от сторон АD, АВ и ВС этого четырёхугольника. Проведём окружность с центром О и радиусом, равным расстоянию от точки О до прямой АВ. Этот круг касается сторон АD, АВ и ВС данного четырёхугольника. Докажем, что круг касается и стороны СD. Пусть СD 1 – вторая касательная, проведённая из точки С (рис. 76). Тогда по теореме 7
АВ + С D1 = ВС + АD 1. (2)
Если точка D принадлежит отрезку АD 1, то
CD < DD 1 + CD 1. (3)
Вычтя из равенства (2) равенство (1), получим СD 1 – CD = АD 1 – АD, или, учтя, что АD 1 – АD = DD 1, СD 1 – CD = DD 1, что противоречит условию (3).
Если же точка D 1 принадлежит отрезку АD, то
CD 1 < DD 1 + CD. (4)
После вычитания равенства (2) из равенства (1) получим С D – CD 1 = АD – АD 1, или, с учётом того, что АD – АD 1 = DD 1: СD – CD 1 = DD 1 что противоречит (4).
Поэтому точки D и D 1 совпадают.
Теорема 9. Если четырёхугольник АВСD описан около круга с центром О, то
Ð AОВ + Ð ВОC = 180º, Ð AОD + Ð ВОC = 180º.
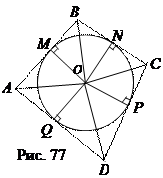 Доказательство. Пусть точки M, N, P, Q – точки касания сторон четырёхугольника АВСD и вписанного в него круга с центром О (рис. 77). Тогда из равенств
Доказательство. Пусть точки M, N, P, Q – точки касания сторон четырёхугольника АВСD и вписанного в него круга с центром О (рис. 77). Тогда из равенств
D АОМ = D АОQ, D ВОМ = D ВОN,
D СОN = D СОР, D DОP = D DОQ получим:
Ð AОМ = Ð AОQ, Ð BОМ = Ð BОN, Ð CОP = Ð CОN,
Ð DОP = Ð DОQ, откуда
Ð AОB + Ð СОD = Ð AОМ + Ð BОM + Ð CОP + Ð DОP =
= Ð AОQ + Ð BОN + Ð CОN + Ð DОQ = Ð BОC + Ð AОQ.
Поскольку Ð AОB + Ð СОD + Ð BОC + + Ð AОD = 360º, то Ð AОВ + Ð ВОC = Ð AОD + Ð ВОC = 180º.
Date: 2015-05-05; view: 1907; Нарушение авторских прав