Теорема косинусов

3.1. Теорема косинусов является одной из наиболее используемых теорем при решении задач на треугольники. Это:

а) найти сторону треугольника, если известны две другие стороны и угол между ними;

б) найти угол треугольника, если известны три его стороны;

в) найти сторону треугольника, если известны прилежащий к ней угол и две другие стороны.

Задачи а) и б) использованы при решении задачи 1.1.

Задача в), в отличии от задач а) и б), которые всегда решаются однозначно, может иметь 2 решения, 1 решение или ни одного (рис. 3, 4, 5)

В задаче в) даны стороны а и с и угол А, прилежащий к неизвестной стороне АС. Рисунки 3, 4, 5 показывают, как можно построить треугольник АВС по этим элементам и возможные исходы этого построения. Рассмотренная задача на построение треугольника АВС соответствует алгебраической задаче на решение квадратного уравнения

b ² – (2с соsÐ А)b + (с ² – а ² ) = 0,

которое может иметь 2 решения (рис. 3), 1 решение (рис. 4), 0 решений (рис. 5).

3.2. Рассмотрим применение теоремы косинусов.

Теорема 1. Треугольник является остроугольным, прямоугольным или тупоугольным в зависимости от того, меньше, равен или больше квадрат его большей стороны по сравнению с суммой квадратов двух других его сторон.

Доказательство основывается на равенстве соs C = .

Теорема 2. Сумма квадратов диагоналей параллелаграмма равна сумме квадратов всех его сторон.

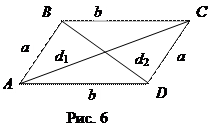Доказательство. Применив к треугольникам АВС и АВD (рис. 6) теорему косинусов, будем иметь:

d 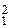= a ² + b ² – 2 ab cos Ð ABC,

d = a ² + b ² – 2 ab cos Ð BAD.

Сложив эти равенства, получим

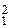d + d = 2a ² + 2b ² – 2ab( cos Ð ABC + cos Ð BAD) =

= 2 a ² + 2 b ², поскольку cos Ð ABC + cos Ð BAD = cos ( 180^° – Ð BAD) + cos Ð BAD =

= – cos Ð BAD + cos Ð BAD = 0.

Следствие 1. Квадрат медианы треугольника равен полусумме квадратов сторон, между которыми проходит эта медиана, уменьшенный на квадрат половины стороны, к которой проведена эта медиана:

m = –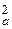

Доказательство. Продолжим медиану АМ за точку М на такое же расстояние: МА ₁ = АМ (рис. 7). Тогда АВА ₁ С – параллелограмм, и a ² + (2 m_a)² = 2 b ² + 2 c ², откуда m = – .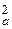

Теорема 3 (Стюарта). Для произвольной точки D на стороне ВС треугольника АВС выполняется равенство

АВ ² DC + AC ² BD – AD ² BC = BD DC BC.

Доказательство. Из треугольников АDС и АDВ будем иметь AC ² = AD ² + DC ² – 2 AD DC cos Ð ADC,

AB ² = AD ² + BD ² – 2 AD BD cos Ð ADB.

Учитывая, что Ð ADB = 180° – Ð ADC, и умножив равенства соответственно на BD и DC и сложив их почленно, получим

AB ² DC + AC ² BD = (AD ² + BD ² – 2 AD BD cos (180 ° –Ð ADC)) DC + (AD ² +DC ² –

– 2 AD DC cos Ð ADC) BD = AD ² DC + BD ² DC + 2 AD BD DC cos Ð ADC +

+ AD ² BD + DC ² BD – 2 AD BD DC cos Ð ADC = AD ² (DC + BD) +

+ BD DC (BD + DC) = AD ² ·BC + BD DC BC, откуда

АВ ² DC + AC ² BD – AD ² BC = BD DC BC.

Date: 2015-05-05; view: 905; Нарушение авторских прав