Из треугольника АВС по теореме косинусов

Раздел 1. Алгебраический метод

Сущность алгебраического метода

Алгебраический метод применяется при решении задач, в которых по данным величинам нужно найти другие, искомые величины.

Задача 1. Стороны треугольника равны 5, 6, 8 (рис. 1). На сторонах длиной 5 и 6 выбраны точки М и N соответственно так, что ВМ: МА = 4: 1, BN: NC = 1: 2. Найти длину отрезка МN.

Решение.

Поскольку 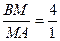, , 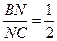то ВМ = 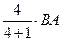= = = 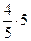4, ВN = 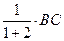= = 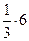2.

Из треугольника АВС по теореме косинусов

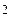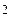АС = ВА + ВС 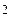– 2 ВА ВС соsÐ В,

или соsÐ В = = = – = – .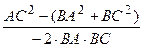

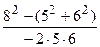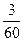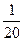Из треугольника МВN по теореме косинусов:

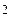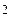МN = BM + BN 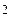– 2 BM BN cosÐ B = 4 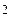+ 2 – 2 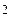4 2 (– 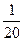) = 16 + 4 + 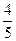= 20,8, откуда МN = 2 .

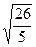При решении задачи 1 проводилось поэтапное вычисление, при котором из данных величин через вычисления ряда промежуточных найдена искомая величина. При этом были использованы известные геометрические факты.

Задача 2. На сколько треугольных частей можно разрезать тысячеугольник, в котором отмечены 500 внутренних точек, если вершинами треугольников могут быть только вершины тысячеугольника и отмеченные точки.

Решение.

Пусть после разрезания возникло х треугольных частей. Сумма их внутренних углов равна 180 х. Поскольку до разрезания треугольников эти углы составляли все внутренние углы тысячеугольника и все полные углы с вершинами в отмеченных точках, то их сумма равна

180 (1000 – 2) + 360 500. Поэтому

180 х = 180 (1000 – 2) + 360 500,

или х = 998 + 1000, или х = 1998.

Отметим, что вместе с ответом на вопрос задачи, мы доказали, что количество частей – треугольников не зависит от способа разрезания.

При решении задачи 2 неизвестная величина найдена с помощью уравнения, которое было составлено с учетом условия задачи и известных геометрических фактов.

Date: 2015-05-05; view: 977; Нарушение авторских прав