Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Примеры движений
|
|
У п р а ж н е н и е 1. Найти формулы параллельного переноса. Доказать, что праллельный перенос является движением первого рода. Определить неподвижные точки и неподвижные прямые при параллельном переносе. Доказать, что множество всех праллельных перносов является группой.
У п р а ж н е н и е 2. Поворотом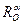 
плоскости вокруг точки 
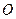на угол 
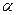называется отображение плоскости в себя, при котором точка 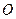переходит сама в себя, любая другая точка 
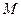плоскости переходит в точку 
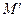такую, что расстояния 
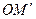и 
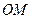равны и угол 
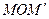равен .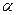
Задав на плоскости прямоугольную систему координат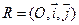 
, выразите косинус и синус угла 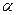через косинусы и синусы углов 
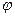и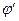 
, образованных векторам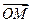и 
и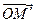 
с вектором 
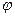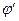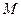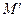. Далее выразите косинусы и синусы углов и через координаты точек и . Убедитесь, что
, 
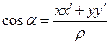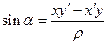, где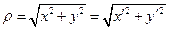 
.
Решая систему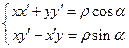 
относительно 
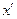и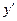 
, получим формулы поворота 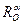вокруг начала координат: 
.
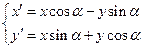Убедиться, что поворот вокруг точки является движением первого рода. Определить неподвижные точки при повороте. Выяснить, что представляет собой поворот на угол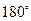 
. Доказать, что множество всех поворотов с общим центром является группой. Найти формулы поворота вокруг точки 
.
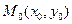У п р а ж н е н и е 3. Осевой с имметрией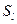 
с осью 
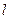называется отображение плоскости в себя, при котором каждой точке плоскости ставится в соответствие точка, симметричная ей относительно прямой .
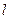Напомним, что каждая точка прямой 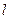симметрична сама себе. Точка, не лежащая на прямой 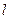, и симметричная ей точка определяют отрезок, перпендикулярный прмой 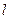, середина которого лежит на прямой .
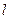Найдите формулы симметрии относительно оси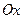 
, убедитесь, что осевая симметрия является примером движения второго рода. Найдите неподвижные точки, неподвижные прямые при осевой симметрии. Выясните, что представляет собой композиция двух осевых симметрий с параллельными осями, с пересекающимися осями.
У п р а ж н е н и е 4. Скользящей симметрией называется композиция осевой симметрии и параллельного переноса на вектор, параллельный оси симметрии: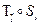 
.
Показать, что скользящая симметрия является движением второго рода, отличным от осевой симметрии.
Определить неподвижные точки и неподвижные прямые при скользящей симметрии.
Date: 2015-05-04; view: 828; Нарушение авторских прав