Движения плоскости, их свойства

Преобразование плоскости, сохраняющее расстояния, называется движением (перемещением) плоскости.

Примеры движений

1. Тождественное преобразование.

2. Параллельный перенос.

Параллельным переносом на вектор 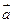называется отображение плоскости в себя, при котором каждой точке 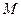плоскости ставится в соответствие точка 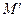такая, что .

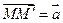a) Отметим, что параллельный перенос определяется как отображение и, следовательно нужно доказать, что он является преобразованием плоскости (сделайте это самостоятельно).

b) Имеем 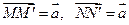. Тогда 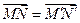и 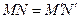, то есть параллельный перенос сохраняет расстояния, а значит является движением плоскости.

3. Центральная симметрия.

Центральной симметрией 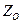относительно точки 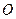называется отображение плоскости в себя, при котором каждой точке 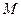плоскости ставится в соответствие точка 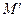такая, что .

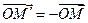a) Аналогично нужно показать, что центральная симметрия является преобразованием плоскости.

b) Из услови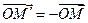й и 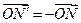получаем, что 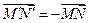. Тогда 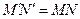, то есть центральная симметрия сохраняет расстояния, а значит, является движением плоскости.

Самостоятельно следует рассмотреть доказательство следующих важных теорем

Т е о р е м а 1. При движении образом репера является репер. Образом оротнормированного репера является ортонормированный репер.

Т е о р е м а 2. (о задании движения парой соответствующих ортонормированных реперов) Пусть 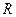и 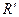два ортонормированных репера. Существует единственное движение плоскости, которое репер 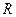переводит в репер 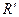. При этом движении каждая точка 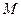с координатами 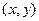в репере 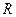переходит в точку 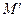с теми же координатами в репере .

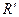Теоремы 1-2 позволяют доказать следующие свойства движений:

1. Движение переводит прямую в прямую, праллельные прямые в параллельные прямые.

2. Движение переводит полуплоскость в полуплоскость.

3. Движение сохраняет простое отношение трех точек прямой, а значит сохраняет отношение «лежать между», а значит переводит отрезок в отрезок, луч в луч, угол в угол.

4. Движение переводит угол в равный угол, перпендикулярные прямые в перпендикулярные прямые.

5. Любое движение либо сохраняет ориентацию плоскости (любой репер переводит в одинаково ориентированный с ним репер), либо меняет ориентацию плоскости (любой репер переводит в противоположно ориентированный с ним репер).
Отсюда имеем два вида движений: движения I рода (сохраняющие ориентацию плоскости) и движения II рода (меняющие ориентацию плоскости).

Date: 2015-05-04; view: 2337; Нарушение авторских прав