Свойства подобий

Т е о р е м а 1. (о разложении подобия в композицию гомотетии и движения) Всякое преоборазование подобия можно представить как композицию гомотетии с тем же коэффициентом и движения.

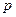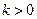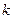Д о к а з а т е л ь с т в о. Пусть – подобие с коэффициентом . Если – гомотетия с коэффициентом , то 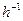– гомотетия с коэффициентом 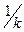. Тогда композиция 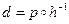является движением и мы имеем 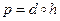– представление подобия в виде композиции гомотетии с тем же коэффициентом и движения.

Из этой теоремы и свойств гомотетии и движения получаем свойства подобий:

1. Подобие переводит прямую в прямую.
2. Подобие сохраняет простое отношение трех точек прямой, а значит, сохраняет отношение «лежать между» и отрезок переводит в отрезок, луч в луч, угол в угол, полуплоскость в полуплоскость.
3. Подобие переводит угол в равный угол.
4. Существуют подобия I и II рода.
5. Множество Р всех подобий плоскости является группой относительно композиции преобразований. Подгруппами этой группы являются: группа 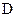всех движений плоскости, множество всех гомотетий с общим центром, множество всех гомотетий и параллельных переносов.
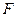6. Фигуры и называются подобными, если они эквивалентны относительно группы Р подобий. Примерами подобных фигур являются два треугольника, соответственные стороны которых пропорциональны, два эллипса (две гиперболы), эксцентриситеты которых равны, любые две параболы.