Параболоиды

О п р е д е л е н и е. Поверхность, полученная вращением параболы вокруг её оси, называется параболоидом вращения.

Пусть в пространстве задана прямоугольная система координат 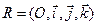и в плоскости 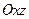в репере 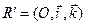парабола задана каноническим уравнением 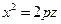. Чтобы получить параболоид вращения, достаточно рассмотреть одну ветвь параболы, заданную уравнением .

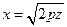Поверхность, полученная при вращении этой линии вокруг оси 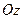, будет задаваться уравнением 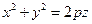– каноническое уравнение параболоида вращения.

О п р е д е л е н и е. Поверхность, полученная из параболоида вращения путем сжатия к плоскости, проходящей через ось вращения, называется эллиптическим параболоидом.

Выполнив сжатие к плоскости 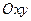, получим каноническое уравнение эллиптического параболоида:

.

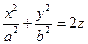Исследование эллиптического параболоида методом сечений:

1. Из уравнения следует, что плоскости 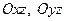являются плоскостями симметрии, а ось 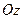– осью симметрии.

2. При пересечении эллиптического параболоида с плоскостью 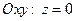получаем точку 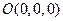– вершина эллиптического параболоида.

3. При пресечении эллиптического параболоида с плоскостью 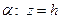, параллельной плоскости 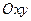, получаем эллипс (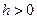) или мнимый эллипс ().

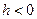4. При пересечении эллиптического параболоида с плоскостью 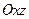или плоскостями ей параллельными (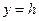), получаем параболы 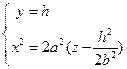с одним и тем же фокальным параметром . То есть это будут одинаковые параболы, расположенные в параллельных плоскостях.

5. Аналогично, при пересечении эллиптического параболоида с плоскостью 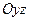и параллельными ей плоскостями, будем получать одинаковые параболы с фокальным параметром .

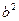Из пунктов 4 и 5 исследования эллиптического параболоида методом сечений следует другой способ получения эллиптического параболоида.

Пусть 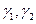– две параболы с общей вершиной, общей осью, расположенные в перпендикулярных плоскостях, и их ветви направлены в одну сторону. Тогда, поверхность, полученная смещением одной параболы параллельно самой себе так, что её вершина скользит по другой параболе, будет эллиптическим параболоидом.

Пусть 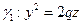– неподвижная парабола, а 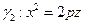– подвижная парабола. Можно показать, что координаты любой точки 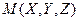поверхности Ф, образованной смещением 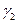параллельно самой себе так, что её вершина скользит по параболе 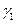, и только координаты этих точек будут удовлетворять уравнению 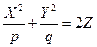. То есть поверхность Ф является эллиптическим параболоидом.

Если 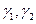– две параболы с общей вершиной, общей осью, расположенные в перпендикулярных плоскостях, и их ветви направлены в противоположные стороны, то уравнение поверхности Ф, полученной смещением одной параболы параллельно самой себе так, что её вершина скользит по другой параболе, будет иметь вид 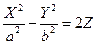или 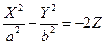. Поверхность, задаваемая таким уравнением, называется гиперболическим параболоидом (сечения плоскостями, параллельными координатным плоскостям, являются либо гиперболами, либо параболами).

Date: 2015-05-04; view: 721; Нарушение авторских прав