Гомотетия как пример преобразования подобия

О п р е д е л е н и е. Подобием с коэффициентом 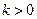называется преобразование плоскости, при котором все расстояния умножаются на .

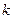Примеры подобий

1. Любое движение является подобием с коэффициентом .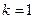

2. Гомотетией 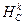с центорм 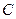и коэффициентом 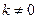называется отображение плоскости в себя, при котором каждой точке 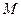ставится в соответствие точка 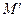такая, что .

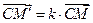Проверить, что гомотетия является биективным отображением, а значит, является преобразованием плоскости.

Для любых двух точек 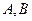и их образов 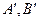при гомотетии имеем 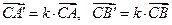. Тогда 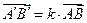и 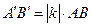, то есть гомотетия с коэффициентом 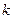является подобием с коэффициентом .

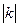Из условия 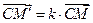получаем формулы гомотетии

,

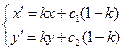позволяющие доказать свойства гомотетии:

a. При гомотетии прямая, не проходящая через центр гомотетии, переходит в параллельную ей прямую, а прямая, проходящая через центр гомотетии – в себя.

b. Гомотетия сохраняет простое отношение трех точек прямой, а значит, сохраняет отношение «лежать между» и отрезок переводит в отрезок, луч в луч, угол в угол.

c. Гомотетия переводит угол в равный угол (Почему?).

d. Гомотетия сохраняет ориентацию плоскости. Для доказательства этого свойства находим по формулам гомотетии координаты точек, определяющих репер 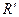– образ репера 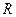при гомотетии. Затем находим координаты базисных векторов репера 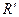и убеждаемся, что определитель матрицы перехода от базиса репера 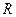к базису репера 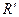равен 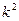, то есть реперы 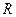и 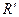одинаково ориентированы.

Date: 2015-05-04; view: 850; Нарушение авторских прав