Формулы движений

Пусть 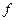– движение плоскости. Задав на плоскости прямоугольную систему координат 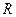, сможем найти формулы движения 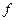: это формулы, выражающие координаты 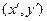точки 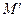через координаты 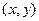точки 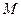– прообраза точки .

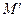Пусть при движении 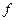ортонормированный репер 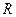переходит в ортонормированный репер 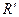. Тогда по теореме 2 о задании движения парой ортонормированных реперов следуент, что 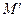имеет координаты 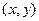в репере .

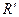Рассматривая 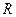и 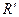как старую и новую системы координат, получаем, что точка 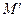имеет соответственно старые координаты 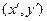относительно репера 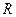и новые координаты 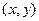относительно репера 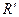. Используя формулы преобразования координат при переходе от одной системы координат к другой, получим

(*),

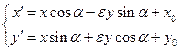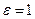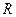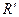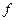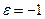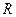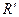где , если и одинаково ориентированы, то есть – движение первого рода, и , если и противоположно ориентированы, то есть 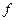– движение второго рода.

Формулы (*) это и есть формулы движения. Можно заметить, что матрица, составленная из коэффициентов пр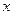и и в этих формулах, является ортогональной (сумма квадратов элементов одного и того же столбца равна 1, а сумма произведений соответствующих элементов разных столбцов равна 0); определитель этой матрицы равен 1 в случае движения первого рода и равен -1 в случае движения второго рода.

Имеет место следующая теорема

Т е о р е м а 3. (об аналитическом задании движения) Пусть 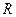– ортонормированный репер. Формулы

(**),

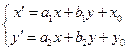где 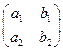– ортогональная матрица, определяют движение первого рода, если определитель этой матрицы равен 1 и второго рода, если определитель этой матрицы равен -1.

При доказательстве этой теоремы следует обосновать три момента:

1. Формулы действительно задают преобразование плоскости (проверить биективность).

2. Преобразование 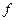сохраняет расстояния (вычисляя расстояние между точкам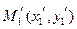и и 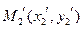, использовать формулы (**) и условие ортогональности матрицы, составленной из коэффициентов, показать, что ).

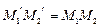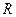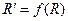3. Показать, что реперы и одинаково ориентированы, то есть 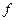является движением первого рода, если 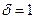и противоположно ориентированы, то есть 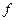– движение второго рода, если 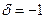. Для этого, используя формулы (**) нужно найти координаты точек 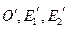образов точек 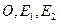, определяющих репер 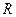. Далее найти координаты векторов 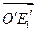и 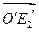и убедиться, что матрица перехода от базиса 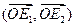к базису 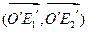имеет вид 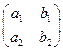. Знак определителя этой матрицы характеризует одинаковость ориентации этих базисов, а значит и реперов 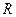и .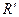

Date: 2015-05-04; view: 1334; Нарушение авторских прав