Аффинная система координат в пространстве

Раздел III. Аналитическая стереометрия

Лекция 1. Плоскость в пространстве как поверхность первого порядка. Задание полупространства. Расстояние от точки до плоскости

Аффинная система координат в пространстве

О п р е д е л е н и е. Аффинной системой координат в пространстве (аффинным репером) называется точка и три некомпланарных вектора: .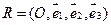

Прямые 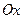, , 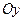, 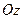определяемые точкой 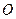и векторами 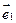, , 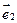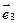называются соответственно осью абсцисс, осью ординат и осью аппликат.

Частным случаем аффинной системы координат является прямоугольная система координат 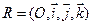, определяемая точкой 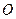и ортогональными ортами .

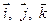О п р е д е л е н и е. Вектор 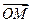называется радиус-вектором точки .

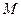О п р е д е л е н и е. Координатами точки называются координаты её радиус-вектора:

.

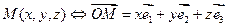У п р а ж н е н и е. Построить точку по координатам в заданном аффинном репере в пространстве.

Аналогично тому, как это делалось на плоскости, с помощью координат решаются простейшие задачи

1. Определение координат вектора по координатам начала и конца в аффинной системе координат.

2. Определение координат точки по заданному простому отношению трех точек прямой и координатам двух из них в аффинной системе координат.

3. Вычисление расстояния между точками по координатам относительно прямоугольной системы координат .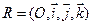

Задавая в пространстве аффинную систему координат, мы устанавливаем взаимно однозначное соответствие между точками и упорядоченными тройками действительных чисел. Это позволяет находить условие, определяющее геометрическую фигуру.

Под условием, определяющим геометрическую фигуру, понимаем упорядоченные тройки действительных чисел, уравнения, неравенства или их системы, которым удовлетворяют координаты любой точки, принадлежащей фигуре, и не удовлетворяют координаты точек, не принадлежащих фигуре.

Тогда геометрическую задачу можно перевести на язык алгебры, решить методами алгебры и полученный результат интерпретировать геометрически.

Date: 2015-05-04; view: 1416; Нарушение авторских прав