Поле равномерно заряженной сферы радиуса R

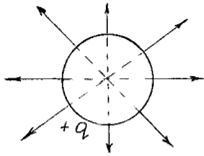
Пусть полный заряд сферы равен q.

Шаг 1. Очевидно, поле сферы выглядит так:

(мы не знаем еще, есть ли поле внутри сферы, поэтому нарисовали линии пунктиром).

Шаг 2. Выбираем сферическую поверхность произвольного радиуса r > R, центр которой совпадает с центром заряженной сферы. Поток через эту поверхность

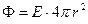(1).

Шаг 3. По теореме Остроградского-Гаусса

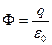(2).

Шаг 4. Сопоставляя выражения (1) и (2) для потока, получаем уравнение:

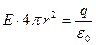, откуда

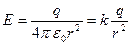
Мы видим, что поле снаружи от заряженной сферы выглядит так, как если бы весь заряд был расположен в центре сферы.

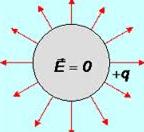
Внутри равномерно заряженной сферы 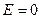(рассуждения такие же, как в предыдущем примере).

4. Поле равномерно заряженного по объёму шара радиуса R

Пусть полный заряд сферы равен q. Заряд, приходящийся на единицу объема (объемная плотность заряда) .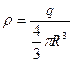

Шаг 1. Как и в предыдущем примере, поле центрально-симметрично, т.е. 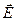во всех точках пространства направлено вдоль радиусов-векторов, а его модуль зависит только от расстояния r от центра.

Шаг 2. Поток через сферическую поверхность произвольного радиуса r, центр которой совпадает с центром заряженного шара,

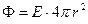(1).

Шаг 3. Найдем сначала поле снаружи от шара. Пусть r > R. Тогда заряд внутри поверхности равен q, а поток

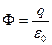(2).

Поэтому 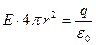. Как и в предыдущем примере, поле снаружи оказывается таким же, как если бы весь заряд был расположен в центре:

.

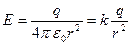Найдем теперь поле внутри шара. Пусть r < R. Тогда заряд внутри поверхности равен 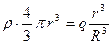, а поток

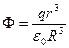(2а).

Сопоставляя (1) и (2а), получаем уравнение:

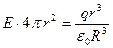, откуда .

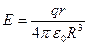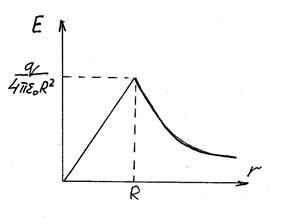
Зависимость Е от r показана на графике:

Мы рассмотрели все основные типы случаев, когда с помощью теоремы Остроградского-Гаусса можно найти напряженность электрического поля.

Увеличить «ассортимент» можно с помощью принципа суперпозиции полей.

Примером могут служить, например, такие комбинации заряженных тел:

а) несколько концентрических заряженных сфер,

б) несколько коаксиальных заряженных длинных цилиндров;

и) несколько параллельных бесконечных заряженных плоскостей.

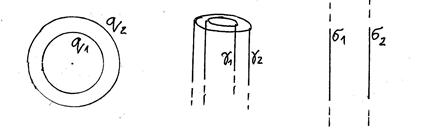
Еще один пример применения теоремы Остроградского-Гаусса:

Теорема о невозможности устойчивого равновесия заряда в электростатическом поле (теорема Ирншоу)

Любая равновесная конфигурация неподвижных точечных зарядов неустойчива, если на них не действуют никакие силы, кроме кулоновских.

Доказательство смотрите в книге «Электромагнетизм. Задачи и решения», задача 1.39.

Date: 2015-05-04; view: 1164; Нарушение авторских прав