Понятие потока. Теорема Остроградского-Гаусса

Определение. Поток вектора 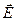через элемент поверхности 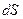- это скалярная величина, равная .

Очевидно, 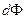> 0, если угол между нормалью и вектором 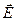острый; 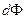< 0, если угол тупой, 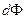=0, если .

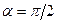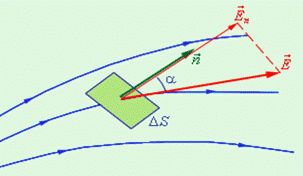
Замечание: элемент поверхности 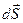считают вектором, направленным по нормали 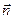к поверхности.

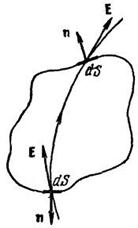Если поверхность замкнута, то выбирается внешняя нормаль.

Для расчета потока Ф через замкнутую поверхность надо брать интеграл по поверхности:

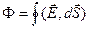
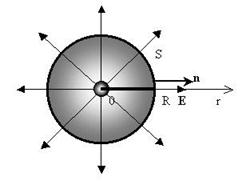Пример. Рассчитаем поток вектора 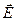через сферическую поверхность радиуса R, в центре которой находится точечный заряд q.

Линии 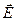в каждой точке поверхности образуют угол 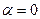с направлением внешней нормали; .

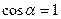Модуль напряженности одинаков в каждой точке поверхности и равен 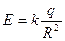. Поэтому

.

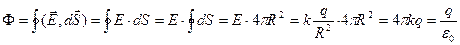Мы видим, что поток не зависит от радиуса сферы. И это напрямую связано с законом обратных квадратов для электрического взаимодействия.

Рассчитать поток поля точечного заряда через замкнутую поверхность какой-либо другой формы было бы гораздо сложнее.

Но можно доказать следующую очень важную теорему.

Date: 2015-05-04; view: 722; Нарушение авторских прав