Теорема Остроградского-Гаусса. Поток вектора через произвольную замкнутую поверхность равен алгебраической сумме зарядов внутри этой поверхности

Поток вектора 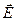через произвольную замкнутую поверхность равен алгебраической сумме зарядов внутри этой поверхности, делённой на :

.

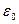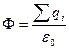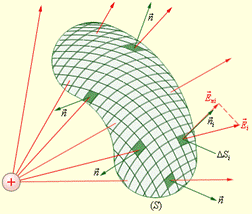
Так, например, поток через поверхност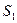и и 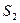, схематически изображенные на рисунке, одинаков и равен 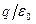, а поток через поверхность 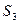равен нулю, т.к. внутри нее заключены заряды 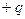и .

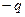Доказательство этой теоремы опирается на два фундаментальных факта: закон Кулона и принцип суперпозиции.

Доказательство.

1) Сначала докажем утверждение для поля одного точечного заряда.

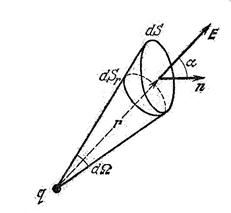
Окружим заряд произвольной замкнутой поверхностью S. Найдем поток d Ф через элемент поверхности dS:

.

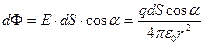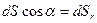- это проекция площадки dS на плоскость, перпендикулярную радиусу-вектору 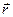, а отношение 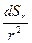есть телесный угол 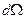с вершиной в точке расположения заряда q, опирающийся на площадку dS. Таким образом,

.

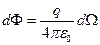Интегрирование потока по всей поверхности сводится, таким образом, к интегрированию по полному телесному углу:

.

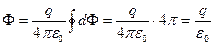2) Пусть внутри поверхности находятся несколько зарядов 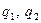…. В каждой точке пространства 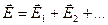. Поток через элемент поверхности

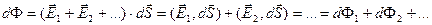
Поэтому полный поток

.

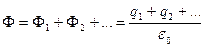Обратите внимание: в то время как поле 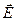зависит от расположения зарядов и меняется при их перемещении, поток Ф зависит только от суммарного заряда внутри поверхности.

Геометрический смысл потока. Поток пропорционален числу силовых линий, пронзающих поверхность, причем линии входящие в поверхность надо считать со знаком плюс, а выходящие – со знаком минус:

Ф 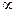число входящих линий – число выходящих линий

Если внутри поверхности нет зарядов, линии не могут кончаться или начинаться внутри неё, поэтому число входящих линий равно числу выходящих, и поток равен нулю.

Date: 2015-05-04; view: 711; Нарушение авторских прав