Применение теоремы Остроградского-Гаусса к расчету полей

В некоторых случаях теорема Остроградского-Гаусса позволяет очень просто найти напряженность поля. Число таких случаев, однако, очень невелико.

1. 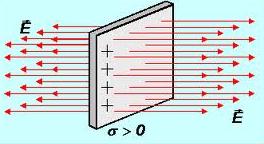Поле бесконечной равномерно заряженной плоскости.

Пусть поверхностная плотность заряда плоскости равна 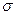. Это значит, что на любом участке плоскости площадью S находится заряд .

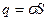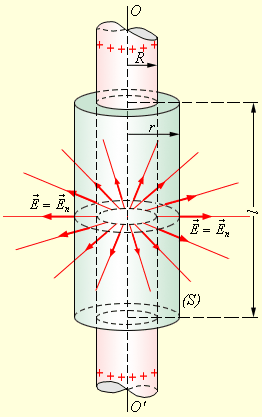
Шаг 1. Прежде всего, попробуем нарисовать линии напряженности. Линии начинаются на зарядах плоскости и могут идти только перпендикулярно к ней – из соображений симметрии. Из рисунка видно, что поле однородно: лини нигде не сгущаются. Значит, напряженность Е одинакова 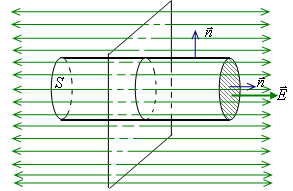по модулю во всех точках пространства.

Обратите внимание: мы смогли сделать этот вывод только на основании симметрии задачи.

Шаг 2. Выбираем такую замкнутую поверхность, поток через которую легко можно рассчитать. В данном случае такой поверхностью является цилиндр (см. рис.) Пусть площадь оснований цилиндра S. Лини напряженности скользят по боковой поверхности цилиндра (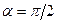), не создавая потока через неё. Поток же через оба торца положителен (линии выходят) и равен

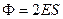. (1)

Шаг 3. Применим теперь теорему Остроградского-Гаусса. Заряд 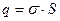оказался внутри цилиндра; весь остальной заряд – снаружи. Поэтому поток

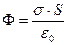. (2)

Шаг 4. Сопоставляя выражения (1) и (2) для потока, получаем уравнение:

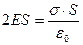, откуда

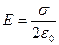
Date: 2015-05-04; view: 1014; Нарушение авторских прав